Carrés latins
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 19 Déc 2022, 14:23
par mathelot » 19 Déc 2022, 14:23
Bonjour,
soit G un ensemble à n éléments.

Un carré latin est une matrice nxn où chaque élément de G intervient une fois et une seule sur chaque ligne et chaque colonne.
Existe-t-il des carrés latins qui ne soient pas une loi de composition de groupe ?
Pour n =4,j'en ai pas trouvé. Je vais essayer de construire le carré autour d'un triplet verifiant
*z \neq x*(y*z))
merci pour votre aide.
Modifié en dernier par mathelot le 19 Déc 2022, 18:08, modifié 1 fois.
-
mathelot
 par mathelot » 19 Déc 2022, 16:12
par mathelot » 19 Déc 2022, 16:12
re-bonjour,

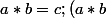*c=c^2=a ; b*c=d ; a*(b*c)=a*d =b)
La loi de composition n'est pas associative. Ce carré latin d'ordre 5x5 n'est pas une loi de groupe.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Déc 2022, 16:27
par GaBuZoMeu » 19 Déc 2022, 16:27
-
mathelot
 par mathelot » 19 Déc 2022, 16:38
par mathelot » 19 Déc 2022, 16:38
ah, oui,joli, merci GBZM
-
mathelot
 par mathelot » 19 Déc 2022, 18:20
par mathelot » 19 Déc 2022, 18:20
mathelot a écrit:re-bonjour,

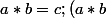*c=c^2=a ; b*c=d ; a*(b*c)=a*d =b)
La loi de composition n'est pas associative. Ce carré latin d'ordre 5x5 n'est pas une loi de groupe.
On sait que si (G,*) est une loi de composition (interne) associative, s'il existe un élément neutre à gauche et si tout élément possède un inverse à gauche, alors (G,*) est un groupe. Le carré ci-dessus , où la loi n'est pas associative , est un contre exemple. L'associativité est nécessaire pour la propriété ci-dessus.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Déc 2022, 19:10
par GaBuZoMeu » 19 Déc 2022, 19:10
Le carré 3x3 que j'ai donné est aussi un contre-exemple.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
