J'ai lu dans le sujet "Centrale Maths 2 PC 2018" que, si deux variables
Je voudrais démontrer cette affirmation et voici mon idée :
donc
Qu'en pensez-vous ? Je ne suis pas pleinement satisfait, j'ai l'impression de gruger un peu...
Caractérisation de la loi d'une variable discrète
5 messages
- Page 1 sur 1
Caractérisation de la loi d'une variable discrète
par SuperPoule » 15 Juil 2025, 17:38
Bonjour,
J'ai lu dans le sujet "Centrale Maths 2 PC 2018" que, si deux variables
et 
à valeurs dans 
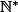
vérifient : pour tout =P(Y\in a\N^*))
, alors et suivent la même loi.
Je voudrais démontrer cette affirmation et voici mon idée :
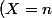 = (X\in n\N^*)\cap \overline{\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)})
donc
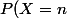 = P\left((X\in n\N^*)\cap \overline{\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)}\right) = P\left((Y\in n\N^*)\cap \overline{\bigcup\limits_{k=2}^{+\infty}(Y\in kn\N^*)}\right) = P(Y=n))
Qu'en pensez-vous ? Je ne suis pas pleinement satisfait, j'ai l'impression de gruger un peu...
J'ai lu dans le sujet "Centrale Maths 2 PC 2018" que, si deux variables
Je voudrais démontrer cette affirmation et voici mon idée :
donc
Qu'en pensez-vous ? Je ne suis pas pleinement satisfait, j'ai l'impression de gruger un peu...
Re: Caractérisation de la loi d'une variable discrète
par GaBuZoMeu » 15 Juil 2025, 20:18
Bonsoir,
Comment justifies-tu la deuxième égalité de la deuxième ligne ?
Comment justifies-tu la deuxième égalité de la deuxième ligne ?
Re: Caractérisation de la loi d'une variable discrète
par SuperPoule » 15 Juil 2025, 22:29
Bonjour GaBuZoMeu,
Merci pour ta réponse.
Oui, c'est à cause de cette égalité-là que je ne suis pas pleinement satisfait...
Je dirai : grâce à l'hypothèse "pour tout", je vois bien que ce n'est pas très clair..
Merci pour ta réponse.
Oui, c'est à cause de cette égalité-là que je ne suis pas pleinement satisfait...
Je dirai : grâce à l'hypothèse "pour tout
Re: Caractérisation de la loi d'une variable discrète
par GaBuZoMeu » 16 Juil 2025, 08:09
Comment exprimes-tu ton \cap \overline{\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)}\right))
en fonction des )
?
Re: Caractérisation de la loi d'une variable discrète
par SuperPoule » 16 Juil 2025, 11:54
Voici les idées qui me viennent :
1) 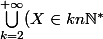\subset(X\in n\N^*))
, donc :
\cap \overline{\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)}\right) = P( X\in n\N^*) - P\left(\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)\right))
2) Le théorème de la limite monotone : 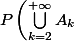= \lim\limits_{k\to+\infty}P\left(\bigcup\limits_{i=2}^{k}A_k\right))
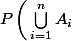3) La version probabiliste du crible de Poincaré :=\sum_{S\subset[\![2,n]\!],\,S\neq\varnothing} (-1)^{|S|-1}\ P\left(\bigcap_{i\in S}\,A_{i}\right))
4) On pose, pour tout entier
: )
.
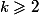
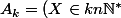A partir de là, on a :
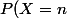 = P(A_1) - \lim\limits_{k\to+\infty} \sum_{S\subset[\![2,k]\!],\,S\neq\varnothing} (-1)^{|S|-1}\ P\left(\bigcap_{i\in S}\,A_{i}\right))
5) Enfin, pour tout
, on a : 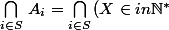 = (X\in ppcm(S)n\N^*))
.
Donc = P(X\in ppcm(S)n\N^*) = P(Y\in ppcm(S)n\N^*))
, ce qui permettrait de conclure... J'ai bon ?
1)
2) Le théorème de la limite monotone :
3) La version probabiliste du crible de Poincaré :
4) On pose, pour tout entier
A partir de là, on a :
5) Enfin, pour tout
Donc
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :