Calculer une somme de 2manieres
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
flo1012
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Sep 2006, 18:30
-
 par flo1012 » 29 Sep 2006, 18:40
par flo1012 » 29 Sep 2006, 18:40
Bonjour je suis en prepa BCPST et je bloque sur un DM j'aurais besoin d'un peu d'aide:
On se propose de calculer par 2méthodes différentes
Sn=somme de k=0 à n de k*(k parmi n)
1ére méthode: f(x) (1+x)puissance n
calculer f'(x) de 2maniéres différentes. En déduire Sn.
Je vois bien une méthode pour calculer f'(x) mais je ne vois pas de 2éme!
2éme méthode: vérifier que pour tout k de N étoile
k(k parmi n)= n((k-1) parmi (n-1)); en déduire Sn.
Merci d'avance et bonne soirée.
-
smaths
- Membre Naturel
- Messages: 35
- Enregistré le: 21 Juin 2006, 19:45
-
 par smaths » 29 Sep 2006, 23:15
par smaths » 29 Sep 2006, 23:15
Bonsoir,
=(1+x)^n)
=n(1+x)^{n-1})
=\sum_{k=0}^{n} C_{n}^{k}x^k)
Calculer la dérivée de cette expression et conclure.
-
flo1012
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Sep 2006, 18:30
-
 par flo1012 » 30 Sep 2006, 13:24
par flo1012 » 30 Sep 2006, 13:24
Bonjour,
Je vois bien la transformation de f par la formule du Binôme, mais je ne vois pas comment dériver une somme ? :s

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 30 Sep 2006, 14:06
par nuage » 30 Sep 2006, 14:06
Salut,
la dérivée d'une somme est la somme des dérivées de chaque terme de la somme.
-
flo1012
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Sep 2006, 18:30
-
 par flo1012 » 30 Sep 2006, 15:26
par flo1012 » 30 Sep 2006, 15:26
Oui donc j'ai trouvé f'(x)= somme de k=0 à n de k*(k parmi n)*x(puissance k-1) mais ça ne m'aide pas pour trouver Sn si ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 30 Sep 2006, 15:28
par nuage » 30 Sep 2006, 15:28
Un conseil : calcule f'(1)
-
flo1012
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Sep 2006, 18:30
-
 par flo1012 » 30 Sep 2006, 15:51
par flo1012 » 30 Sep 2006, 15:51
Oui je trouve f'(1)=1 mais en quoi ça peut m'aider ? :triste:

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 30 Sep 2006, 16:03
par nuage » 30 Sep 2006, 16:03
Salut,

flo1012 a écrit:Oui je trouve f'(1)=1 mais en quoi ça peut m'aider ? :triste:

Quand je remplace x par 1 dans
^{n-1})
je ne trouve pas 1, mais

ce qui n'est pas la même chose (sauf si n=1).
De même en remplaçant x par 1 dans
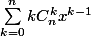
-
flo1012
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Sep 2006, 18:30
-
 par flo1012 » 01 Oct 2006, 10:06
par flo1012 » 01 Oct 2006, 10:06
Oupq oui c'est ce que j'avais trouvé pour le 1er mais ça me semblait bizarre :s! Sinon ça peut m'aider comment pour déduire Sn ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
