Calculer le terme du rang n

[Pauly]

Bonjour,

on considère la suite (Un)n>=0 dont les termes successifs sont 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6... calculer en fonction de n, le terme de rang n.

Pourriez-vous me donner quelques pistes pour commencer merci.

[zygomatique]

Bonjour,

on considère la suite (Un)n>=0 dont les termes successifs sont 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6... calculer en fonction de n, le terme de rang n.

Pourriez-vous me donner quelques pistes pour commencer merci.

salut



....

[nodjim]

La partie entière par excés de la racine carrée de 2n doit donner une bonne approximation de Un.

[Pauly]

J'ai pas trop compris comment on calcule le terme au rang n

[jlb]

J'ai pas trop compris comment on calcule le terme au rang n

Suppose écris ta liste jusqu'à p entier (tu as écris p p ... p , p fois) il y a combien de nombres écris dans cette liste?

1+2+3+...+p cela te dit quelque chose?

[nodjim]

Un= partie entière par excés de rac(2n+1/4)-1/2
Bon, t'es bien avancé avec ça....

[Pauly]

jlb : 1+2+3+...+p=(p+1)p/2

nodjim : Je ne vois pas comment on obtient rac(2n+1/4)-1/2

[nodjim]

ça vient du fait que, au rang r=n(n+1)/2, on trouve Ur=n et qu'au rang suivant U(r+1)=n+1.

[chan79]

salut
j'arrive à

[Pauly]

Je n'arrive pas à trouver rac(2n+1/4)-1/2
J'comprends pas vraiment pourquoi on prend les termes d'une somme arithmétique (n(n+1)/2)

[BiancoAngelo]

Je n'arrive pas à trouver rac(2n+1/4)-1/2
J'comprends pas vraiment pourquoi on prend les termes d'une somme arithmétique (n(n+1)/2)

Parce qu'on a 1 fois 1 qui apparaît + 2 fois 2 qui apparaît + 3 fois 3 qui apparaît...

Donc pour arriver au 4, il faut avoir "lu" 1 + 2 + 3 termes et le suivant est bien un 4...

[Pauly]

Ah d'accord
Mais comment avoir ce fameux terme?

[BiancoAngelo]

Ah d'accord
Mais comment avoir ce fameux terme?

C'est tout ce qu'écrivent les intervenants sur le poste... Relis tout en ayant compris ce que je viens de t'écrire
Je n'apporterai rien de vraiment mieux que ce qui est écrit...
A part détailler en phrases...

Établis une formule qui à un entier p donné donne la valeur n telle que pour la première fois...

[zygomatique]

il est clair que la première occurrence de n apparaît au rang 1 + 2 + 3 + ... + (n - 1) + 1


....

désolé pour mon premier post qui ne traduit absolument pas ce que je voulais dire .... comme au dessus ....

[Pauly]

BiancoAngelo : ça te dérangerait de détailler un peu plus parce que je comprends vraiment pas, je ne vois pas comment la racine apparaît

[BiancoAngelo]

BiancoAngelo : ça te dérangerait de détailler un peu plus parce que je comprends vraiment pas, je ne vois pas comment la racine apparaît

Comme vient de dire zygomatique, on a pour la première fois quand .

Donc pour .

Qu'on peut noter ainsi : et c'est la première fois que la suite vaut n.

Cette notation, plutôt moyenne, nous amène à :

.
.
Donc .

Pourquoi on fait ça ? Car on veut n en fonction de p, et pas l'inverse.

J'ai du second degré, je calcule

Des solutions existent pour notre problème, sans me poser de question je prends :



Donc ce que je viens d'écrire c'est que :

uniquement pour le p qui est l'indice de la première apparition du terme n...

Donc, pour les indices suivants, à savoir p+1,p+2, etc. on sait que cette fraction doit rester égale à n, à savoir entière, et ne changer qu'en p + n, car on aura .

Ce qui signifie qu'il faut prendre la partie entière sur cet intervalle et donc finalement pour tout entier.

On trouve alors :



Sachant que c'est pour la suite commençant à n = 1.

Pour celle indicée en commençant à 0, on trouve bien :

annoncée dans les posts d'avant !

[Pauly]

Là je vois avec vos aides mais je n'aurais jamais pensé à ça tout seul...

[chan79]

Une variante






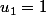
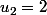
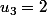
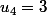
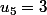
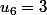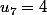
puisque

...
puisque
est égal au nombre entier naturel tel que:
Pour déterminer p, on a les deux inéquations:


Pour les deux,

s'annule pour a et b
s'annule pour c et d








on vérifie facilement que a<c<b<d
Compte tenu des inéquations, l'entier p doit être dans l'intervalle (on a d-b=1)

si est entier, alors

sinon

exemples
pour n=78, d=13 donc
pour n=84, d=13.47... donc

[nodjim]

C'est curieux que selon qu'on travaille avec le 1er terme d'une série ou le dernier, on ait 2 formules assez dissemblables.
Un= E par excès (rac(2n+1/4)-1/2)
Un=E ((1+rac(1+8n)/2)

[chan79]

C'est curieux que selon qu'on travaille avec le 1er terme d'une série ou le dernier, on ait 2 formules assez dissemblables.
Un= E par excès (rac(2n+1/4)-1/2)
Un=E ((1+rac(1+8n)/2)

c'est ce que j'avais remarqué :zen: