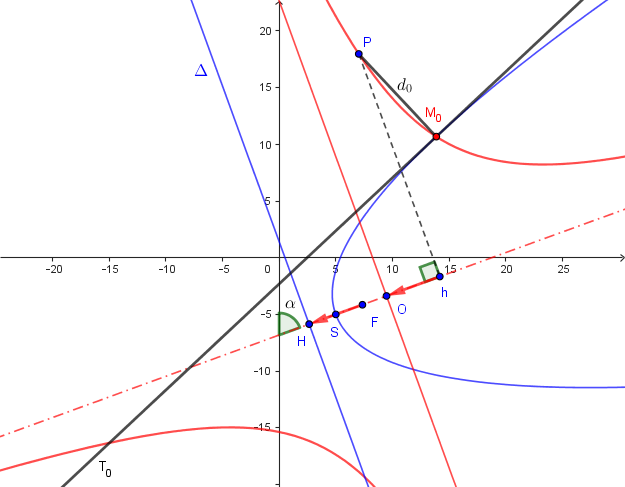
j'ai une parabole d'équation :
0 = a * (cos(theta) * (x-sommet.x) - sin(theta) * (y-sommet.y))^2- sin(theta) * (x - sommet.x) - cos(theta) * (y - sommet.y)
et je cherche la distance minimale de cette parabole avec le point P(xP,yP)
j'ai essayé de faire un code en C++ grâce à l'équation de Ben mais ça ne marche pas, je précise que ma fonction
resoutEquationTroisiemeDegre fonctionne
voici mon code :
- Code: Tout sélectionner
double Parabole::distance(Point2d point) {
double X = point.x - sommet.x;
double Y = point.y - sommet.y;
X = X * cos(theta_radians) - Y * sin(theta_radians);
Y = X * sin(theta_radians) + Y * cos(theta_radians);
vector<double> res = resoutEquationTroisiemeDegre(2 * pow(a, 2),0, 1 - 2 * a * Y, -X);
double minimum = std::numeric_limits<double>::infinity();
for (int k = 0; k < res.size(); k++) {//pour chaque solution complexe
double t = res[k];
double delta = pow(t - X, 2) + pow(a * pow(t, 2) - Y, 2);
if (delta < minimum)
minimum = delta;
}
return sqrt(minimum);
}