Calcule d'aire

[pseudodupseudo]

Bonsoir,

pourriez vous m'aider pour un exercice que je ne comprend pas.
Soit A dans R² que l'on délimite par et .
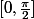
:-> R²


Je dois dessiner A ainsi que calculer son aire.
Pourriez vous m'indiquer comment on doit faire pour que je comprenne.

je pense que pour le dessin j'ai un quart de cercle, non ?

Je vous remercie d'avance

[deltab]

Bonjout.

Bonsoir,

pourriez vous m'aider pour un exercice que je ne comprend pas.
Soit A dans R² que l'on délimite par et .
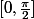
:-> R²


Je dois dessiner A ainsi que calculer son aire.
Pourriez vous m'indiquer comment on doit faire pour que je comprenne.

je pense que pour le dessin j'ai un quart de cercle, non ?

Je vous remercie d'avance

Est-tu sûr que c'est un quart de cercle?

[pseudodupseudo]

Non je viens de m'apercevoir de la bêtise que j'ai dit.
Je dirais plus précisément que j'ai 1/4 d'ellipse passant par (1;0) et (0;2) et de centre (0;0)

[pseudodupseudo]

Non je viens de m'apercevoir de la bêtise que j'ai dit.
Je dirais plus précisément que j'ai 1/4 d'ellipse passant par (1;0) et (0;2) et de centre (0;0)

mais pour l'aire je ne sais pas qu'elle est la démarche à suivre

[pseudodupseudo]

un peu d'aide svp ?

[mrif]

Tu as les coordonnées paramétriques de la courbe que tu peux transformer en coordonnées cartésiennes:
sin(u) est positif sur l'intervalle de définition, donc , ce qui donne:


La question revient à calculer l'aire délimitée par la courbe, l'axe des x, et les droites x=0 et x= 1, puisque x appartient à [0;1], ce qui revient à calculer l'intégrale:

[deltab]

Bonsoir.

un peu d'aide svp ?

Utilises le changement de variables , . Que valent et dans ton cas. N'oublies pas ensuite le jacobien.

[pseudodupseudo]

J'ai une autre méthode à proposer:
si je dit que j'ai:
donc,









= /2

pensez vous que c'est juste svp ?

cela me donne le même résultat qu'avec le méthode de mrif

[deltab]

J'ai une autre méthode à proposer:
si je dit que j'ai:
donc,









= /2

pensez vous que c'est juste svp ?

cela me donne le même résultat qu'avec le méthode de mrif

sauf que dans tu n'as rien donné concernant sur quoi tu intègres.

[pseudodupseudo]

sauf que dans tu n'as rien donné concernant sur quoi tu intègres.

A vrai dire j'ai rien mis car je ne sais pas quoi mettre.
Je dirais que c'est également sur 0 pi/2.
Est ce juste svp ?

[chan79]

A vrai dire j'ai rien mis car je ne sais pas quoi mettre.
Je dirais que c'est également sur 0 pi/2.
Est ce juste svp ?

Salut
On a une ellipse d'équation
l'aire du quart de cette ellipse est

[pseudodupseudo]

Salut
On a une ellipse d'équation
l'aire du quart de cette ellipse est

A vrai dire je suis censé utilisé les intégrales vue que c'est le chapitre étudié. Mais je me met de côté la formule, merci

[mrif]

J'ai une autre méthode à proposer:
si je dit que j'ai:
donc,









= /2

pensez vous que c'est juste svp ?

cela me donne le même résultat qu'avec le méthode de mrif

Quand tu écris (j'ai ajouté les bornes: y varie de 0 à 1), tu supposes que x est une fonction de y, c'est comme si tu écrivais sans donner l'expression de f. Cela revient à passer en coordonnées cartésiennes sans le dire.

[pseudodupseudo]

Merci de votre explication car j'avais un peu de mal.

Petite question:

est ce que je peux utiliser la formule suivante ou c'est une formule qui correspond à des "situations particulières":

Aire= 1/2 intégrale (x dy -y dx)
car je retrouve pi/2

[mrif]

Je ne sais pas d'où sort cette formule.
Je te conseille de n'utiliser que ce que tu as appris.
Tu es au lycée ou dans le supérieur?

[pseudodupseudo]

Je ne sais pas d'où sort cette formule.
Je te conseille de n'utiliser que ce que tu as appris.
Tu es au lycée ou dans le supérieur?

J'ai trouvé cette formule à la fin de cet article wikipédia: ici

je suis dans le supérieur

pour le cours, ils nous donnent la base et le reste, c'est du travail personnel d'où le fait que c'est encore un peu vague pour moi cette notion du chapitre

[mrif]

En quelle année dans le supérieur et quelle branche?

[deltab]

A vrai dire j'ai rien mis car je ne sais pas quoi mettre.
Je dirais que c'est également sur 0 pi/2.
Est ce juste svp ?

L'intégrale est en fait une intégrale curviligne c.à.d qu'on intègre sur une courbe. C'est la formule de Green-Riemann qui va donner le résultat. Si on prend pour C le contour fermé formé par le quart de l'ellipse et les 2 segments l'un vertical , l'autre horizontal , on aura alors .
Soit le domane délimité par C, la formule de Green-Riemann donne et cette dernière est bien l'aire de

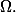
Le résultat final est exact en tant que valeur car les 2 intégrales et sont nulles , ce que tu as omis de préciser, l'intégrale que tu as calculée est .

[pseudodupseudo]

En quelle année dans le supérieur et quelle branche?

En deuxième année de prépa intégré en école d'ingénieur généraliste.


merci de l'explication deltab

[chan79]

Je ne sais pas d'où sort cette formule.
Je te conseille de n'utiliser que ce que tu as appris.
Tu es au lycée ou dans le supérieur?

pour une ellipse avec et comme demi-axes (équation)

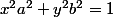
l'aire est
je crois que c'est connu.
Si ce n'est pas le cas, bien-sûr, on utilise le cours :zen: