Calcul d'une somme d'exponentielle

[pat_74]

Bonjour,

On me demande de calculer l'expression A suivante



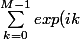puis de calculer le maximum de sachant que la fonction
prend son maximum en zéro.

Mon problème et que je ne vois pas le rapport entre f et A. Quelqu'un peut il m'expliquer comment calculer A pour arriver à f ?

Merci

[Cheche]

Salut,

Pour le calcul de l'expression A, il s'agit de la somme d'une suite géométrique de raison : q = exp(i) = -1. Tu sais donc la calculer.

Et pour le rapport entre l'expression A et la fonction, utilise peut-être :

sin(x) = (exp ix - exp -ix) / (2i)

[girdav]

Bonjour.
Il y a quand même quelque chose qui m'échappe.
donc .
Je crois qu'on demande plutôt
sinon il n'y aurait pas de maximum car serait constant.

[uztop]

Bonjour,

non la fonction est et pas ; elle n'est pas donc pas egale a

[girdav]

Exact: donc la raison est et la somme est constante pour fixé. A ne semble pas dépendre de

[uztop]

euh si, la somme depend bien de M. Tu trouves quoi ?
Sinon, oui pour M fixe elle est constante vu qu'elle ne depend que de M

[girdav]

D'accord dans ce cas le maximum demandé est en fonction de M entier. En quoi l'indication sur un maximum qui dépend de (réel a priori) peut-elle nous être utile?

[uztop]

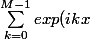la somme que tu dois considérer ne serait pas par hasard ?