[Résolu]Calcul d'une limite.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 07 Déc 2007, 22:31
par diablos » 07 Déc 2007, 22:31
Bonjour. J'ai un petit exercice a faire c'est de cherche la limite de
 = \frac {n^{2}-{\sqrt{(n^{4}-7)}}}{6n^{2}-{\sqrt{(36n^{4}-1)}})
Si je comprend bien il faut faire le developpement limite d'ordre 1 (car les autres on a pas fait encore) du therme d'en haut puis de selui du bas et faire la limite??
Si c'est ca j'essaye d'appliquer la formule suivante
f(xo) + f'(x0)(x - x0) + (x - x0)E(x) mais le probleme ce que le premier therme f(x0) c'est impossible de l'avoir vu que il est impossible d'avoir un racine d'un nombre negatif

J'aimerais un petit coup de pouce svp si possible.
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 07 Déc 2007, 22:35
par muse » 07 Déc 2007, 22:35
je ne comprend a peu rien a ce que tu dis a la fin...
mais tu as f(x) qui ne depent pas de x pour moi c'est une constante ... donc je supose que tu t'es tromper c'est x et pas n ?
aussi as tu vu la division polynomiale par ordre decroissant?
-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 07 Déc 2007, 22:43
par diablos » 07 Déc 2007, 22:43
muse a écrit:je ne comprend a peu rien a ce que tu dis a la fin...
mais tu as f(x) qui ne depent pas de x pour moi c'est une constante ... donc je supose que tu t'es tromper c'est x et pas n ?
aussi as tu vu la division polynomiale par ordre decroissant?
Euh non je ne crois pas. On m'as dis qu'il faut le faire avec le developpement limite d'ordre 1 cette limite.
P.S: Oui je me suis trompe je retifie

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Déc 2007, 23:09
par fatal_error » 07 Déc 2007, 23:09
Bonjour,
je n'ai pas compris ce que représente ta fonction f dans la formule de taylor lagrange, tu peux cependant faire rentrer les n dans la racine et tout devient plus facile
la vie est une fête

-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 07 Déc 2007, 23:39
par diablos » 07 Déc 2007, 23:39
Je ne vois pas comment on peut mettre les n dans le racine?
Par contre ce uqe j'ai essaye de faire c'est de sortir les n de la racine. Du coup ca me donne a la fin
}}{6n^{2}(1-\sqr{1+\frac{1}{36n^{4}})})
Mias je ne vois toujours pas commment avoir la limite de ce machin.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 08 Déc 2007, 00:42
par fatal_error » 08 Déc 2007, 00:42
Oui de toute façon on s'est compris!
Il ne te reste plus qu'a faire un developement limité de tes racines.
tu pose x=1/n^4
n>infini =>x=>0 et tu peux appliquer taylor lagrange sur sqrt(1-x) par exemple.
la vie est une fête

-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 08 Déc 2007, 12:29
par diablos » 08 Déc 2007, 12:29
fatal_error a écrit:Oui de toute façon on s'est compris!
Il ne te reste plus qu'a faire un developement limité de tes racines.
tu pose x=1/n^4
n>infini =>x=>0 et tu peux appliquer taylor lagrange sur sqrt(1-x) par exemple.
Voila c'est la justement la qu'il y a un probleme ce que je ne sais pas comment l'appliquer. Esque je peux avoir un exemple svp pour que j'essaye??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 08 Déc 2007, 12:56
par tize » 08 Déc 2007, 12:56
Bonjour,
En zéro,
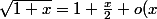)
donc par exemple :
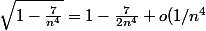)
-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 08 Déc 2007, 13:07
par diablos » 08 Déc 2007, 13:07
tize a écrit:Bonjour,
En zéro,
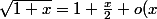)
donc par exemple :
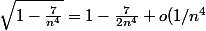)
Pouvez vous me developper unpeu le seconde developpement car j'arrive pas a comprendre comment on trouve ca avec la formule de taylor.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 08 Déc 2007, 13:14
par fatal_error » 08 Déc 2007, 13:14
Tize a simplement posé x=-7/n^4
Il a ensuite remplacé x par sa valeur dans sqrt(1+x).
la vie est une fête

-
diablos
- Membre Naturel
- Messages: 13
- Enregistré le: 28 Nov 2006, 12:33
-
 par diablos » 08 Déc 2007, 13:33
par diablos » 08 Déc 2007, 13:33
Donc si j'ai bien compris apres je fais pareil pour le denominateur:
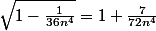
puis je remplace dans l'equation du debut qui me fait:
)}{6n^{2}(1-(1+\frac{7}{72n^{4}}))})
Puis je developpe et ca me donne la limite a la fin??
Edit: oui c'est ca merci pour vous reponces. J'ai trouve la limite qui est egale a 42. Merci a tous pour votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
