Calcul d'une limite..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chronosis
- Messages: 3
- Enregistré le: 30 Nov 2007, 13:45
-
 par chronosis » 06 Déc 2007, 16:15
par chronosis » 06 Déc 2007, 16:15
Bonjour je poste ce message car je n'arrive pas à trouver cette limite :
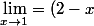^{tan(pi*\frac{x}{2})})
Tout d'abord je l'ai posé sous forme d'exponnetielle donc ca me donne :
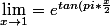ln(2-x)})
mais je n'y arrive pas , je sais qu'il faut que je me débrouille pour mettre un X pour qu'il tende vers 0 mais je ne voit pas du tout comment faire car quand je pose x= X+1 ca revient au même et je trouve une forme indeterminée.
Il parait que le resultat est

Merci d'avance.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 06 Déc 2007, 16:38
par fatal_error » 06 Déc 2007, 16:38
bonjour, j'imagine que la FI est due à la tangente...
il faut faire le DL du cosinus et du sinus puis faire le quotient
la vie est une fête

-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 06 Déc 2007, 16:58
par Pythales » 06 Déc 2007, 16:58
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 06 Déc 2007, 18:07
par Lierre Aeripz » 06 Déc 2007, 18:07
fatal_error a écrit:bonjour, j'imagine que la FI est due à la tangente...
il faut faire le DL du cosinus et du sinus puis faire le quotient
Une méthode beaucoup plus rapide pour calculer le DL de la tangente est d'écrire tan' = 1+tan², puis de conclure par unicité du DL.
Peu de gens connaissent cette méthode, c'est bien dommage...
-
chronosis
- Messages: 3
- Enregistré le: 30 Nov 2007, 13:45
-
 par chronosis » 06 Déc 2007, 18:07
par chronosis » 06 Déc 2007, 18:07
pythales je n'ai pas compris à ce que tu as fait ..
Désolé mais ca veut dire quoi la DL merci
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 06 Déc 2007, 18:18
par Babe » 06 Déc 2007, 18:18
chronosis a écrit:pythales je n'ai pas compris à ce que tu as fait ..
Désolé mais ca veut dire quoi la DL merci
DL=developement limité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2007, 18:24
par Nightmare » 06 Déc 2007, 18:24
Bonsoir,
sinon on écrit que :
=e^{tan(\pi \frac{x}{2})ln(2-x)}=e^{sin(\pi\frac{x}{2})\times \frac{ln(2-x)}{x-1}\times \frac{x-1}{cos(\pi \frac{x}{2})})
Or :
\longrightarrow_{x\to 1} 1)
}{x-2}\longrightarrow_{x\to 1} -1)
(taux d'accroissement)
}\longrightarrow_{x\to 1} -\frac{2}{\pi})
(taux d'accroissement inversé)
Au final notre truc tend vers
\times (-\frac{2}{\pi})=e^{\frac{2}{\pi}})
Q.E.D
:happy3:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 06 Déc 2007, 21:17
par fatal_error » 06 Déc 2007, 21:17
tan' = 1+tan²
J'avoue ne pas très bien comprendre comment utiliser cette méthode.
Serait-il possible d'en avoir un petit exemple?
la vie est une fête

-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 06 Déc 2007, 22:16
par Lierre Aeripz » 06 Déc 2007, 22:16
Mettons que tu veuille un DL à l'ordre 7.
Premièrement, tangente est impair et on sait déjà qu'il est équivalent à x en zéro, d'où
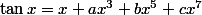
. (J'omet les 'grand O').
Donc
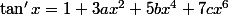
et
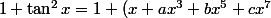^2 = 1 + x^2 + 2a x^4 + (2b+a^2) x^6)
Tu as donc, en identifiant les coefficients, a = 1/3, b = 2/15 et c = 17/315.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Déc 2007, 09:40
par fatal_error » 07 Déc 2007, 09:40
merci,
j'avoue que c'est une technique sympathique!
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
