calculer la limite suivante
sin(picos(x))/xsin(x) quand x tend vers 0 .
ps: l'editeur d'equation ne marche pas chez moi je sais pas pq
Calcul d'une limite
8 messages
- Page 1 sur 1
Re: calcul d'une limite
par rcompany » 21 Déc 2018, 00:01
As-tu essayé d’appliquer la règle de l’Hopital?
Re: calcul d'une limite
par haithem6 » 21 Déc 2018, 00:10
rcompany a écrit:As-tu essayé d’appliquer la règle de l’Hopital?
l'exercice dit qu'il faut la calculer sans la régle de l'hopital
Re: calcul d'une limite
par rcompany » 21 Déc 2018, 00:26
J'essaierais de trouver un encadrement de la fonction en m'inspirant des développements limités du numérateur et du dénominateur
Re: calcul d'une limite
par Ben314 » 21 Déc 2018, 07:45
Salut,
Ce type d'exo., si on utilise pas la règle de l’Hôpital, alors un truc pas con c'est d'utiliser des taux d'accroissement et des dérivées.
- Pour le\big))
, avec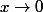 
, on a affaire à du )
avec 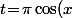\to\pi)
donc ça tend vers \!=\!0)
mais on sait plus précisément que \!-\!\sin(\pi)}{t-\pi}\!=\!\sin'(\pi)\!=\!\cos(\pi)\!=-1)
. Donc \big)}{\pi\cos(x)-\pi}\!=-1)
.
- De même)
avec 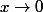tend vers \!=\!0)
mais on sait plus précisément que \!-\!\sin(0)}{x-0}\!=\!\sin'(0)\!=\!\cos(0)\!=\!1)
.
Tout cela conduit naturellement à écrire que :
\big)}{x\sin(x)}=\dfrac{\sin\big(\pi\cos(x)\big)}{\pi\cos(x)-\pi}\!\times\!\dfrac{x}{\sin(x)}\!\times\!\dfrac{\pi(\cos(x)\!-\!1)}{x^2})
Où les deux premiers facteurs ont été "fabriqués" de façon à faire apparaître des taux d’accroissements dont la limite est connu (égale à -1 pour le premier et égale à 1 pour le deuxième) et où le troisième facteur est là pour que le produit des trois termes soit bien égal à l'expression de départ.
Par contre le troisième facteur est un peu plus problématique : On peut écrire le taux d'accroissement de la fonction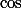
pour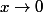 
et on obtient \!-\!\cos(0)}{x-0}\!=\!\cos'(0)\!=-\sin(0)\!=\!0)
c'est à dire \!-\!1}{x}\!=\!0)
sauf que ce n'est pas suffisant pour déterminer la limite de \!-\!1}{x^2}\!=\!\dfrac{\cos(x)\!-\!1}{x}\!\times\!\dfrac{1}{x}\;\mathop{\longrightarrow}\limits_{x\to 0}\; 0\!\times\!\pm\infty)
: forme indéterminée.
Mais il y a une astuce classique normalement vue au Lycée consistant à écrire que :
\!-\!1}{x^2}\!=\!\dfrac{(\cos(x)\!-\!1)(\cos(x)\!+\!1)}{x^2(\cos(x)\!+\!1)}<br />=\dfrac{\cos^2(x)\!-\!1}{x^2(\cos(x)\!+\!1)}<br />=\dfrac{-\sin^2(x)}{x^2(\cos(x)\!+\!1)}<br />=\Big(\dfrac{\sin(x)}{x}\Big)^{\!2}\!\times\!\dfrac{-1}{\cos(x)\!+\!1}\cr<br />\ \ \ \ \ \ \ \ \ \ \ \ \mathop{\longrightarrow}\limits_{x\to 0}\ 1^2\!\times\!\dfrac{-1}{1+1}=-\dfrac{1}{2})
Ce type d'exo., si on utilise pas la règle de l’Hôpital, alors un truc pas con c'est d'utiliser des taux d'accroissement et des dérivées.
- Pour le
- De même
Tout cela conduit naturellement à écrire que :
Où les deux premiers facteurs ont été "fabriqués" de façon à faire apparaître des taux d’accroissements dont la limite est connu (égale à -1 pour le premier et égale à 1 pour le deuxième) et où le troisième facteur est là pour que le produit des trois termes soit bien égal à l'expression de départ.
Par contre le troisième facteur est un peu plus problématique : On peut écrire le taux d'accroissement de la fonction
Mais il y a une astuce classique normalement vue au Lycée consistant à écrire que :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: calcul d'une limite
par rcompany » 22 Déc 2018, 02:44
Méthode plus laborieuse:
DL de
en 0: \;\;\;\;\;\lim_{x\to 0} {\varepsilon (x)}=0)
DL de en 
: -\frac{(x-\pi)^3}{3!}+\frac{(x-\pi)^5}{5!}+\varepsilon (x)\;\;\;\;\;\lim_{x\to \pi} {\varepsilon (x)}=0)
DL de
en 0: \;\;\;\;\;\lim_{x\to 0} {\varepsilon (x)}=0)
On définit:
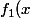= -(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24}))
= -(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24})+\frac{(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24})^3}{3!})
On montre que<\sin{(\pi\cos{x})}<f_1(x))
On définit:
= x^2-\frac{x^4}{3!})
= x^2-\frac{x^4}{3!}+\frac{x^6}{5!})
On montre que<x.\sin{x}<g_2(x), soit\;0<\frac{1}{g_2(x)}<\frac{1}{x.\sin{x}}<\frac{1}{g_1(x)}\;\;pour\;x\neq 0)
On a alors}{g_2(x)}<\frac{\sin{\pi \cos{x}}}{x.\sin{x}}<\frac{f_1(x)}{g_1(x)})
Comme}{g_2(x)}}=\lim_{x\to 0^-}{\frac{-(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24})+\frac{(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24})^3}{3!}}{x^2-\frac{x^4}{3!}+\frac{x^6}{5!}}=\frac{\pi}{2})
et}{g_1(x)}}=lim_{x\to 0^-}{\frac{-(-\pi\frac{x^2}{2}+\pi \frac{x^4}{24})}{x^2-\frac{x^4}{3!}}}=\frac{\pi}{2})
(on factorise dans les 2 cas par )
on en déduit que}}{x\sin{x}}=\frac{\pi}{2})
Même chose pour la limite à droite:}}{x\sin{x}}=\frac{\pi}{2})
et donc}}{x\sin{x}}=\frac{\pi}{2})
Ce qui est surtout laborieux, c'est de retranscrire tout cela en LaTex......
DL de
DL de
DL de
On définit:
On montre que
On définit:
On montre que
On a alors
Comme
et
on en déduit que
Même chose pour la limite à droite:
et donc
Ce qui est surtout laborieux, c'est de retranscrire tout cela en LaTex......
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :