Calcul d'une intégrale impropre

[jonses]

Bonjour ou bonsoir,

J'essaye de calculer cette intégrale :


J'ai déjà justifié son existence (des études locales et en utilisant les règles de domination au voisinage de 0, 1 et prouvent la convergence de cette intégrale[/tex]


Mais ensuite pour calculer, j'ai vraiment du mal.
Je pense que le but est de chercher une primitive de

Et c'est là où je bloque, je me suis emmêlé dans mes calculs et j'ai perdu un temps fou pour aboutir à rien.

Si quelqu'un peut m'aider svp.
Je vous remercie d'avance pour vos réponses

[Pythales]

Bonjour ou bonsoir,

J'essaye de calculer cette intégrale :


J'ai déjà justifié son existence (des études locales et en utilisant les règles de domination au voisinage de 0, 1 et prouvent la convergence de cette intégrale[/tex]


Mais ensuite pour calculer, j'ai vraiment du mal.
Je pense que le but est de chercher une primitive de

Et c'est là où je bloque, je me suis emmêlé dans mes calculs et j'ai perdu un temps fou pour aboutir à rien.

Si quelqu'un peut m'aider svp.
Je vous remercie d'avance pour vos réponses

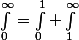
Ecris et dans l'une des intégrales pose

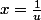
Mais est-ce bien ?

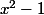
[jonses]

Mais est-ce bien ?

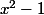
Oui c'est bien x²-1


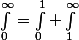
[quote="Pythales"]Ecris et dans l'une des intégrales pose


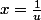
J'ai fait le changement de variable dans la deuxième intégrale, mais du coup tout cela revient à calculer

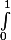
et là aussi je bloque, je n'arrive pas à trouver une primitive de ln(x)/(x²-1) pour pouvoir déterminer la limite de l'intégrale

[Ben314]

Salut,
Si tu suit l'indic. de Pythalés (sans te gourrer dans les calculs évidement...) tu devrait trouver que l'intégrale de départ I=0 sans avoir à calculer l'intégrale de 0 à 1 de ton truc (je ne suis pas persuadé qu'on puisse calculer cette dernière d'ailleurs...)

[vingtdieux]

La fonction a intégrer est toujours positive, donc elle I ne peut être nul.

[BiancoAngelo]

La fonction à intégrer est toujours positive, donc elle I ne peut être nulle.

Effectivement, on trouve bien :



Il y a un signe - qui a du se faire la malle

[BiancoAngelo]

On peut peut-être simplifier un peu du coup en faisant ça :

D'abord, je décompose 1/(x²-1) en éléments simples.
Je trouve que c'est = (1/2)*(1/(x-1)) - (1/2)*(1/(x+1)).

Donc il faut calculer

et .

Après, à voir.

[BiancoAngelo]

Sachant qu'on peut écrire que :



Sauf erreur de ma part.

Je ne sais pas si ça peut aider.

[Ben314]

La fonction a intégrer est toujours positive, donc elle I ne peut être nul.

ln(x) est positif sur ]0,1] ?

[Ben314]

La fonction a intégrer est toujours positive, donc elle I ne peut être nul.

Effectivement :marteau:

[Ben314]

La fonction a intégrer est toujours positive, donc elle I ne peut être nul.

Effectivement :marteau:

Et dans ce cas, c'est passablement la m...
Le seul truc qui me vient à l'esprit, c'est de passer par les séries entières :

En justifiant proprement l'interversion des symboles somme et intégrale et... en ayant un peu de culture générale pour calculer la somme finale...

P.S. Vu la forme "spéciale" du résultat, je me demande s'il y a des moyens "élémentaires" de trouver le résultat...

[BiancoAngelo]

Effectivement :marteau:

Et dans ce cas, c'est passablement la m...
Le seul truc qui me vient à l'esprit, c'est de passer par les séries entières :

En justifiant proprement l'interversion des symboles somme et intégrale et... en ayant un peu de culture générale pour calculer la somme finale...

P.S. Vu la forme "spéciale" du résultat, je me demande s'il y a des moyens "élémentaires" de trouver le résultat...

J'ai essayé pas mal de changements de variable, et effectivement, ce n'est pas trivial...
A mon avis, ce que tu as donné doit être le moyen le plus simple.

[Pythales]

Effectivement :marteau:

Et dans ce cas, c'est passablement la m...
Le seul truc qui me vient à l'esprit, c'est de passer par les séries entières :

En justifiant proprement l'interversion des symboles somme et intégrale et... en ayant un peu de culture générale pour calculer la somme finale...

P.S. Vu la forme "spéciale" du résultat, je me demande s'il y a des moyens "élémentaires" de trouver le résultat...

En intégrant la fonction le long d'un cercle de centre O dont le rayon tend vers l'infini, muni d'une coupure entre et , sachant que les intégrales le long du grand cercle et le long du cercle entourant O tendent vers on arrive à
avec et il reste


L'ennui, c'est que la 2ème intégrale n'est pas nulle (elle est même impropre), sinon on arrive bien au résultat

Mystère ...

[Ben314]

Je pense que, pour que ça fonctionne "bien", de la même façon que tu n'as pas intégré jusqu'à 0, mais en parcourant un petit cercle, il ne faut pas intégrer directement sur [0,+oo[ mais sur des demi-droites un peu au dessus et un peu en dessous de [0,+oo[, en particulier du fait que ton il est pas trop cohérent vu qu'en x=1 ça déconne (donc en fait, à "l'aller", tu peut te placer directement sur l'axe, mais au "retour", il faut décaler de epsilon vers le bas)
En procédant de cette façon, tu devrait facilement montrer proprement que le "soit-disant" est bien nul.

[Pythales]

Je pense que, pour que ça fonctionne "bien", de la même façon que tu n'as pas intégré jusqu'à 0, mais en parcourant un petit cercle, il ne faut pas intégrer directement sur [0,+oo[ mais sur des demi-droites un peu au dessus et un peu en dessous de [0,+oo[, en particulier du fait que ton il est pas trop cohérent vu qu'en x=1 ça déconne (donc en fait, à "l'aller", tu peut te placer directement sur l'axe, mais au "retour", il faut décaler de epsilon vers le bas)
En procédant de cette façon, tu devrait facilement montrer proprement que le "soit-disant" est bien nul.

Je crois que j'ai trouvé.
Il faut intégrer le long du quart de cercle allant de à puis de à puis de à .
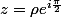
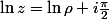
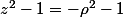
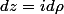
Sur le dernier parcours, soit , et de sorte qu'on a comme précédemment
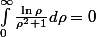
et comme cette fois, il reste finalement

Le résultat est immédiat.