Calcul d'une bijection réciproque

par **Stanley** » 30 Nov 2007, 18:26

Bonsoir à tous,

Voila j'ai un petit problème. Je suis en prépa HEC, et je butte sur un problème. On me fait savoir qu'il n'est absolument pas de mon niveau, mais peut-être que la personne qui m'a dit ça s'est trompé...

Le problème est le suivant :

Calculer la bijection réciproque de f(x)=2*x*exp(x)

Je n'ai vu à ce jour que les suites, le dénombrement, les limites et la continuité. Est-ce qu'il est possible de résoudre ce problème avec ces chapitres et sans faire appel à des equations diférentielles etc. ? ( si oui, la réponse m'interesse, si non, la réponse, bien qu'interessante, ne me serait pas super utile vu que je ne la comrpendrais pas :P )

Par avance, merci à vous et bonne soirée.

par **busard_des_roseaux** » 30 Nov 2007, 21:35

bonsoir,
l'application envoie

non bijectivement. (cf. tableau de variation)

se développe en série entière de

sur

, série dite de Taylor-MacLaurin.

Pour trouver la réciproque sur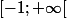

(cf. tableau de variation), j'ai essayé de développer la fonction réciproque en série entière
de y au voisinage de y=0 avec

(dérivée de fonction réciproque)

et d'identifier les coefficients. :briques:

cordialement,

:mur:

par **xyz1975** » 01 Déc 2007, 18:33

Bonsoir,
Il n'est pas possible de trouver la réciproque de cette fonction.

par **ThSQ** » 01 Déc 2007, 18:43

xyz1975 a écrit:Bonsoir,
Il n'est pas possible de trouver la réciproque de cette fonction.

Tu veux dire de l'exprimer avec des fonctions connues simples ?

par **xyz1975** » 01 Déc 2007, 18:45

Evidement, on sait qu'elle existe mais on ne peut pas l'exprimer avec les fonctions usuelles, le developpement en série entière ou Taylor ne répondent pas (notons locales).

par **kazeriahm** » 01 Déc 2007, 18:51

xyz1975 a écrit: le developpement en série entière ou Taylor ne répondent pas (notons locales).

en quoi le fait que le développement de Taylor (ou en série entière) ne soit pas "usuel" justifie le fait que la fonction n'est pas exprimable algèbriquement ?

par **xyz1975** » 01 Déc 2007, 18:52

Je réponds au message posté par "busard_des_roseaux"

par **Stanley** » 01 Déc 2007, 20:05

Merci beaucoup pour vos réponses. Visiblement, cet exercice n'était donc pas du niveau "début de prépa HEC" :hum:
Bonne soirée à tous.

PS : j'ai passer 1h a chercher cette ***** bijection réciproque alors qu'elle n'était pas nécessaire pour faire le DST :cry:

par **busard_des_roseaux** » 01 Déc 2007, 21:08

xyz1975 a écrit:Bonsoir,
Il n'est pas possible de trouver la réciproque de cette fonction.

bonsoir,

tu peux expliquer ?

par **SimonB** » 02 Déc 2007, 02:35

busard_des_roseaux a écrit:bonsoir,

tu peux expliquer ?

Je pense qu'xyz1975 voulait dire qu'on ne peut pas exprimer cette fonction au moyen de fonctions "simples" par produit ou combinaison linéaire. L'exemple typique d'une telle fonction est la primitive de

. Il y a un sujet d'ENS (Lyon-Cachan 95) qui s'intéresse à ça.

par **busard_des_roseaux** » 03 Déc 2007, 21:54

je remonte le fil...
on peut développer la fonction réciproque en série entière de y.

par **busard_des_roseaux** » 03 Déc 2007, 23:03

on a:

on cherche x sous la forme

on obtient:

(on a posé

à cause du 1+x)

on obtient:

quel est le rayon de convergence de cette série ?

Calcul d'une bijection réciproque

Calcul d'une bijection réciproque

Qui est en ligne