Bonjour , j'aimerai exprimé x en fonction de y pour trouver la réciproque de g; mais je bloque; pourriez vous m'aidez à trouver le résultat; svp!
:cry:
on a g(x)=1/2ln|(x-1)/(x+1)|
on pose y=g(x)
2y= ln|(x-1)/(x+1)|
2y= ln (x-1)- ln(x+1)
e^(2y) = (x-1)-(x+1)
Mais du coup j'arrive pas à exprimer x en fonction de y :triste:
Merci pour toute l'aide apportées!
Calcul
11 messages
- Page 1 sur 1
par maeliss » 08 Oct 2008, 20:29
merci josé mais je suis toujours bloqué après je vois par quoi je peut simplifié?? :cry: :cry:
par ericsteph » 08 Oct 2008, 20:59
Salut, etudie ce qu'il ya a l'interieur de la valeur absolue
quand c'est negatif, (...)=-e^2y
quand c'est positif (...)=e^2y
puis c ''est simple, tu peux avoir x en fonction de y
quand c'est negatif, (...)=-e^2y
quand c'est positif (...)=e^2y
puis c ''est simple, tu peux avoir x en fonction de y
par maeliss » 08 Oct 2008, 21:41
nan , je comprend toujours pas! :triste:
qu'elle est le résultat final que je suis censé trouver??
aidez moi je bloque sur ça :cry: :cry:
qu'elle est le résultat final que je suis censé trouver??
aidez moi je bloque sur ça :cry: :cry:
par mathelot » 09 Oct 2008, 07:17
bJR?
Cette fonction est tout à fait intéressante. Il faut que tu l'apprivoise.
As tu remarqué qu'elle était impaire ?
Sa courbe représentative, dans le plan, est la réunion de trois composantes connexes (trois "morceaux"). Trace la.
On voit alors que f réalise une 1ère bijection de
]-1,1[ sur
et une deuxième bijection de
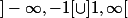sur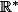 
Assez curieusement, elle va donc admettre deux applications "réciproques",
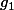et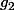 
l'une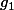, envoyant sur ]-1,1[
On remarque que ces deux ensembles sont des intervalles (parties connexes)
l'autre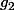, envoyant 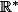sur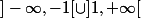 
ces deux derniers ensembles ont chacun deux composantes connexes
puisque ce sont la réunion de deux intervalles.
On va voir de plus que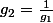
Question calculs:
Le quotient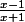
a le même signe que le trinôme (x-1)(x+1), ie, positif pour |x|>1
pour |x|>1)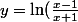
d'où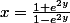 
en multipliant haut et bas par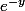
, on trouve:
)
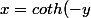, ie, une cotangente hyperbolique.
pour |x|<1
pour |x|<1)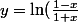
d'où )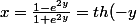
donc une tangente hyperbolique.
Donc voilà la raison cachée de ces belles propriétés: il y a de la trigonométrie hyperbolique là dessous... :zen:
Cette fonction est tout à fait intéressante. Il faut que tu l'apprivoise.
As tu remarqué qu'elle était impaire ?
Sa courbe représentative, dans le plan, est la réunion de trois composantes connexes (trois "morceaux"). Trace la.
On voit alors que f réalise une 1ère bijection de
]-1,1[ sur
et une deuxième bijection de
Assez curieusement, elle va donc admettre deux applications "réciproques",
l'une
On remarque que ces deux ensembles sont des intervalles (parties connexes)
l'autre
ces deux derniers ensembles ont chacun deux composantes connexes
puisque ce sont la réunion de deux intervalles.
On va voir de plus que
Question calculs:
Le quotient
pour |x|>1
en multipliant haut et bas par
pour |x|<1
pour |x|<1
donc une tangente hyperbolique.
Donc voilà la raison cachée de ces belles propriétés: il y a de la trigonométrie hyperbolique là dessous... :zen:
par maeliss » 09 Oct 2008, 07:26
Merci beaucoup j'ai bien compris ton explication; merci d'avoir pris le temps de détaillé. j'aurai jamais trouvé toute seule!
encore une fois MERCI! :we: :happy2:
encore une fois MERCI! :we: :happy2:
par mathelot » 09 Oct 2008, 07:38
on pourrait essayer d'"homogénéiser" tout ça:
sur le domaine de définition de f, on rajoute trois points:
-1, 1 et un point à l'infini
sur l'ensemble d'arrivée on rajoute un point , ce qui donne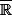 
à ce moment là, la 1ère composante connexe du domaine de définition
de f,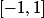
est envoyée sur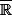
la deuxième composante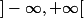
a été connexifiée
par l'ajout d'un point à l'infini
on se récupère alors une application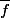
d'un domaine topologiquement équivalent à un cercle fermé
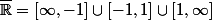sur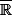 
avec pour chaque y, deux images réciproques
et 
inverses l'une de l'autre.
On doit obtenir ce qu'on appelle en géométrie un revêtement à deux feuillets ?? et en plus, il y aune inversion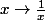
qui fait passer d'une fibre à l'autre. Tout ceci est magnifique.
Bonne journée .
sur le domaine de définition de f, on rajoute trois points:
-1, 1 et un point à l'infini
sur l'ensemble d'arrivée
à ce moment là, la 1ère composante connexe du domaine de définition
de f,
la deuxième composante
par l'ajout d'un point à l'infini
on se récupère alors une application
d'un domaine topologiquement équivalent à un cercle fermé
avec pour chaque y, deux images réciproques
On doit obtenir ce qu'on appelle en géométrie un revêtement à deux feuillets ?? et en plus, il y aune inversion
Bonne journée .
trouver LA fonction ?
par mathelot » 09 Oct 2008, 12:08
re,
on a:)
je subodore qu'il existe une fonction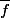
du cercle unité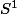
sur lui même
)
et un paramètrage s de sur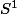
privé d'un point, tel que:
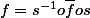
je pensais à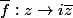
qui échange les axes de la fonction tangente avec les axes de
la cotangente.
mais je n'ai pas trouvé l'expression de
merci d'avance.
on a:
je subodore qu'il existe une fonction
du cercle unité
et un paramètrage s de
privé d'un point, tel que:
je pensais à
qui échange les axes de la fonction tangente avec les axes de
la cotangente.
mais je n'ai pas trouvé l'expression de
merci d'avance.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :