Bonjour,
Je ne parviens pas à aller jusqu'au bout du calcul de la somme suivante:
n
;) (ln((k²+3k+2)/(2k²+3k)))
k=0
On m'indique de factoriser et d'utiliser les propriétés de la fonction ln, mais je n'arrive pas à poursuivre.
J'ai factoriser par k et j'obtiens:
(k²+3k+3)/(k(k+3))
Pouvez me donner des conseils pour poursuivre svp?
Merci
Calcul de sommes avec linéarité et dominos
10 messages
- Page 1 sur 1
Archibald a écrit:Bonjour,
il y a une erreur qui s'est glissée dans votre poste. Vous écrivez d'abordpuis plus loin
.
Ensuite, vous factorisezen
A tout hasard, l'expression initiale ne serait-elle pas :?
Oui j'ai fait des erreurs de frappe... Désolé.
Voici où j'en suis, mais je n'arrive pas à terminer avec le télescopage... :doh:
[quote="Archibald"]Normal, la simplification de l'expression n'est pas du tout terminée 
Autre chose, pas possible que l'indexation commence à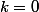 parce qu'alors la division ne serait pas définie.
parce qu'alors la division ne serait pas définie.
(Je vais prendre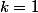 par la suite)
par la suite)
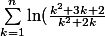 \ = \ \sum_{k=1}^n \ln(\frac{(k+2)(k+1)}{(k+2)k}) \ = \ \sum_{k=1}^n \ln(\frac{k+1}{k}))
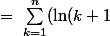-\ln(k)) \ = \ (\ln(2)-\ln(1))+(\ln(3)-\ln(2))+ \cdots + (\ln(n+1)-\ln(n)))
Euh, en fait retour en arrière...
Dans l'expression de départ.. au dénominateur nous avons: k²+3k
Et ça devient tout de suite plus compliqué, en tout cas pour moi*... :mur:
Autre chose, pas possible que l'indexation commence à
(Je vais prendre
Euh, en fait retour en arrière...
Dans l'expression de départ.. au dénominateur nous avons: k²+3k
Et ça devient tout de suite plus compliqué, en tout cas pour moi*... :mur:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
