Calcul de la somme d'une série

par **exilim** » 25 Avr 2007, 15:56

Bonjour a tous !
Voici une question qui me pose problème :
il faut déterminer deux réels

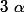
et

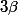
tels que pour tout entier n

on ait

En fait, je n'ai aucune idée de comment démarrer ou de quoi chercher exactement...
Merci de votre aide !

par **tize** » 25 Avr 2007, 16:13

Bonjour,
tu peux essayer de faire 2 I.P.P. , tu trouveras une expression du calcul de l'intégrale pour en déduire ensuite les valeurs de alpha et beta...

par **exilim** » 25 Avr 2007, 16:47

Merci pour le coup de pouce !
je trouve au final:

toutefois, je n'ai pas trop confiance en mes calculs et en mes multiples intégrations par partie, donc si quelqu'un pouvait me dire s'il trouvait comme moi ou pas ca me rassurerait! MERCI

par **tize** » 25 Avr 2007, 16:49

Je suis d'accord pour alpha mais j'ai trouvé beta=1/(2pi) (sans le moins)...
peut être ai-je moi même fait une erreur de calcul... :hein:

par **Joker62** » 25 Avr 2007, 17:09

Donc pour ma part je trouve comme Tize.

par **exilim** » 25 Avr 2007, 17:12

Merci je crois que j'ai trouvé mon erreur !

par **exilim** » 25 Avr 2007, 17:21

j'ai donc réussi la première question ! ce qui ne m'empêche pas de bloquer a la suivante.... :briques:
Il faut déduire de la question précedente que

est un réel indépedant de n ( à préciser )
avec

(j'ai déja prouvé que pour certaines valeurs de t on a

mais je ne vois pas si c'est utile ici)

encore une fois, je ne réchigne pas pour un petit coup de pouce !
MERCI

Calcul de la somme d'une série

calcul de la somme d'une série

Qui est en ligne