Calcul de somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Helidjah
- Membre Naturel
- Messages: 12
- Enregistré le: 26 Jan 2010, 11:15
-
 par Helidjah » 15 Fév 2010, 19:06
par Helidjah » 15 Fév 2010, 19:06
Bonjour à tous,
Je cherche à calculer la somme suivante, définie pour
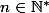
et x > 0 :
[CENTER]
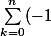^k \frac{n!}{(n-k)!k!} \frac{1}{k+x})
.[/CENTER]
J'ai le résultat suivant en utilisant un logiciel de calcul formel :
[CENTER]
!}{(n+x)!})
.[/CENTER]
Comment prouver l'égalité ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Fév 2010, 19:21
par Nightmare » 15 Fév 2010, 19:21
Salut,
quelle signification donnes-tu à (n+x)! pour x non entier?
-
Helidjah
- Membre Naturel
- Messages: 12
- Enregistré le: 26 Jan 2010, 11:15
-
 par Helidjah » 15 Fév 2010, 19:25
par Helidjah » 15 Fév 2010, 19:25
Pardon, j'aurais dû utiliser la fonction gamma. Prenons comme "résultat" la quantité :
[CENTER]
 \Gamma(x)}{\Gamma(1 + n + x)})
.[/CENTER]
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Fév 2010, 19:37
par Nightmare » 15 Fév 2010, 19:37
Je préfère.
On doit donc calculer
^{k}}{k+x})
Essaye de montrer que cette somme vaut aussi
^{n}dt=B(x,1+n))
où B est la fonction d'Euler.
Ensuite on peut utiliser le résultat
=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)})
(où le redémontrer si on ne le considère pas comme admis. Si tu n'y arrives pas, je te donnerai une esquisse de démonstration, bien que tu puisses en trouver une facilement sur le net je pense).
-
Helidjah
- Membre Naturel
- Messages: 12
- Enregistré le: 26 Jan 2010, 11:15
-
 par Helidjah » 15 Fév 2010, 20:15
par Helidjah » 15 Fév 2010, 20:15
Ah je ne connaissais pas la fonction Bêta.
Merci pour ces indications Nightmare !
Je devrais pouvoir trouver maintenant :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités