Calcul de racine complexe

[Luchir]

Salut,
J'ai un problème avec le calcul d'une racine complexe, pouvez vous me suggerer des piste de recherche:

Il s'agit de calculer les racine de sachant et
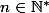
Alors j'ai calculé mais je n'arrive pas à calculer le module :marteau:

[Taupin]

pose donc et ensuite tu sais résoudre z^n = a, normalement

[fatal_error]

Bonjour,

En suivant les conseils de taupin, et supposant que tu cherches le module de x, tu peux te ramener de la forme exponentielle a la forme trigo (cos+isin).

[Taupin]

Hum même pas, enfin c'est presque comme résoudre les racines nième de l'unité quoi, et ensuite comme il y a une bijection en x et z tu conclus ;)

[Luchir]

En fait il s'agit de montrer que les racines de l'équation précédentes sont réelles si =1, si je ne me trompe pas on a en posant on a

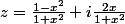
donc z est réelle si

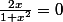
soit x=0
ce qui implique que
=1
or même si x est différent de 0 je trouve ce résultat et la hic !!

[Taupin]

Hein ? Pourquoi tu ne cherche pas simplement les solutions ? :S :marteau:

[Luchir]

en fait c'est l'énoncer de l'exercice qui est comme ca il faut chercher les racines tels qu'elles soient réel

[mathelot]

bjr,
on doit montrer l'équivalence entre:
1) x
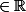
2)

(1) implique (2)

Soit

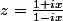
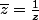
Si x est réel, d' où |z|=1


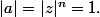
(2) implique (1):
si





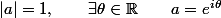
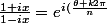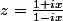
est de module 1

donc

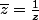
En écrivant cette dernière égalité avec x et un produit en croix:


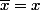
donc x est réel.


Cordialement,

[Luchir]

Excellent ! merci pour la réponse.