Bonjour,
Je n'arrive pas à résoudre ceci :
Soit A une matrice carré d'ordre n où les coefficients diagonaux valent a et tous les autres valent b.
a et b sont réels
Calcule A^n
Faut il décomposer A comme : A= a.IdN + b B avec B la matrice où les coefficients diagonaux valent 0 et tous les autres valent b ?
Je ne vois pas comment continuer
Merci
Calcul puissance d'une matrice
13 messages
- Page 1 sur 1
Re: Calcul puissance d'une matrice
Essaie plutôt avec A =(a-b)I_n et bB où B a tous ses coefficients égaux à 1
Re: Calcul puissance d'une matrice
Bonjour
juste une idée de départ
Soit la matrice d'ordre
la matrice d'ordre  remplie de 1 sauf la diagonale remplie de 0. On écrira
remplie de 1 sauf la diagonale remplie de 0. On écrira  pour
pour  .
.
On trouve queI+(n-2)M)

I+(n-2)M) +2abM=(a^2 +b^2 (n-1))I+(b^2 (n-2)+2ab)M)
On pose
(aI+bM)=u_k aI+(u_k b+v_k a)M+v_k b M^2)
on remplace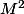
)
)
 \\b & a+b(n-2)\end{pmatrix}=\binom{u_{k}}{v_{k}})


UN EXEMPLE:
avec a=3, b=4 et n=5 la matrice ci-dessus devient

vecteurs propres (1,1) et (-4,1) associés aux valeurs propres 19 et -1


on trouve^4 \end{pmatrix}\begin{pmatrix}0.2 & 0.8 \\-0.2 & 0.2 \end{pmatrix}=\begin{pmatrix}26065 & 104256 \\26064 & 104257 \end{pmatrix})

donc
on peut généraliser le calcul ....
les valeurs propres sont (a-b) et (a-b+bn)
juste une idée de départ
Soit
On trouve que
On pose
on remplace
UN EXEMPLE:
avec a=3, b=4 et n=5 la matrice ci-dessus devient
vecteurs propres (1,1) et (-4,1) associés aux valeurs propres 19 et -1
on trouve
donc
on peut généraliser le calcul ....
les valeurs propres sont (a-b) et (a-b+bn)
Modifié en dernier par chan79 le 19 Sep 2016, 12:00, modifié 1 fois.
Re: Calcul puissance d'une matrice
jlb a écrit:Essaie plutôt avec A =(a-b)I_n et bB où B a tous ses coefficients égaux à 1
Calcule
Utilise le binôme de Newton pour calculer
Re: Calcul puissance d'une matrice
Bonjour;
On a} B) : j'ai remis le B que j'ai oublié à sa place.
: j'ai remis le B que j'ai oublié à sa place.
Supposons que pour .
.
On a donc-1}B) ,
,
donc .
.
On a pour ,
,
etI_n + b B)^m = \sum_{k=0}^m C_m^k b^k(a-b)^{m-k}B^k)
^m I_n + \sum_{k=1}^m C_m^k b^k(a-b)^{m-k}B^k = (a-b)^m I_n + \sum_{k=1}^m C_m^k b^k(a-b)^{m-k}n^{k-1}B)
^m I_n + \frac{1}{n} (\sum_{k=1}^m C_m^k (nb)^k(a-b)^{m-k})B)
^m I_n + \frac{1}{n} (\sum_{k=0}^m C_m^k (nb)^k(a-b)^{m-k} - (a-b)^m)B)
^m I_n + \frac{1}{n} ((nb+a-b)^m - (a-b)^m)B)
^m I_n + \frac{1}{n} (((n-1)b+a)^m - (a-b)^m)B) .
.
Edit: Solution rectifiée suite aux remarques de M. Ben314 .
jlb a écrit:Essaie plutôt avec A =(a-b)I_n et bB où B a tous ses coefficients égaux à 1
On a
Supposons que pour
On a donc
donc
On a pour
et
Edit: Solution rectifiée suite aux remarques de M. Ben314 .
Modifié en dernier par aymanemaysae le 19 Sep 2016, 16:03, modifié 2 fois.
Re: Calcul puissance d'une matrice
aymanemaysae a écrit:Supposons que.
aymanemaysae a écrit:... donc.
BRAVO : ça c'est de la sacré déduction.

Que tu continue à systématiquement donner les solutions des exos. "prêtes à l'emploi", j'ai fini par considérer que c'était pas mon problème : je suis pas modérateur et c'est pas à moi de faire respecter la charte.
Mais par contre, si tu considère que le seul travail devant être fourni par les étudiants pour leur D.M., c'est de recopier ta prose, il me semble que le minimum, ça serait que tu te relise pour éviter les monstruosités telles que celle ci dessus, non ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Calcul puissance d'une matrice
Bonjour,
même si vos propos sont très sévères envers moi, j'ai un grand estime pour vous, et je profite toujours de votre présence pour corriger les monstruosités dont je connais le secret de les produire.
Ce serait vraiment gentil si vous me précisiez mes fautes: c'est un moyen pour progresser.
même si vos propos sont très sévères envers moi, j'ai un grand estime pour vous, et je profite toujours de votre présence pour corriger les monstruosités dont je connais le secret de les produire.
Ce serait vraiment gentil si vous me précisiez mes fautes: c'est un moyen pour progresser.
Re: Calcul puissance d'une matrice
Parce que là, en plus, tu ne voie même pas où est la "monstruosité" ?????
Donc je te la refait en bref :
Y'a rien qui te perturbe ?
P.S. : Perso, c'est surtout le fait de mettre un quelconque laïus entre les deux qui me fait marrer....
Donc je te la refait en bref :
aymanemaysae a écrit:Supposons que la propriété P est vraie (P propriété absolument quelconque)
(laïus...)
Et on en déduit que la propriété P est vrai.
Y'a rien qui te perturbe ?
P.S. : Perso, c'est surtout le fait de mettre un quelconque laïus entre les deux qui me fait marrer....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Calcul puissance d'une matrice
Bonsoir;
J'espère que vous serez patient avec moi, mais il y a des fois que je suis capable des pires des bêtises (monstruosités ici) , mais c'est de bonne foi , comme je suis capable du meilleur. De plus je ne suis pas d'un orgueil maladif, et je sais dire à un Professeur que je n'ai pas compris quand vraiment je n'ai rien compris.
D'abord, je vous remercie pour le terme "laïus" que j'entends pour la première fois. j'ai cherché et j'ai trouvé qu'entre autres définitions ça voulait dire : parler beaucoup pour ne rien dire: pour rire, vous ne m'avez pas vu à l’œuvre, surtout que je suis un adepte de Schopenhauer.
Ensuite, je pense que ma bêtise est si grosse que je n'arrive pas à la voir: je pense que ça consiste l'application de la méthode de récurrence que je ne maîtrise pas encore.
Encore une fois Merci, et un autre Merci si vous daigner me montrer avec une loupe ma bêtise, sinon j'aurai peur d'user de la récurrence dans la futur.
J'espère que vous serez patient avec moi, mais il y a des fois que je suis capable des pires des bêtises (monstruosités ici) , mais c'est de bonne foi , comme je suis capable du meilleur. De plus je ne suis pas d'un orgueil maladif, et je sais dire à un Professeur que je n'ai pas compris quand vraiment je n'ai rien compris.
D'abord, je vous remercie pour le terme "laïus" que j'entends pour la première fois. j'ai cherché et j'ai trouvé qu'entre autres définitions ça voulait dire : parler beaucoup pour ne rien dire: pour rire, vous ne m'avez pas vu à l’œuvre, surtout que je suis un adepte de Schopenhauer.
Ensuite, je pense que ma bêtise est si grosse que je n'arrive pas à la voir: je pense que ça consiste l'application de la méthode de récurrence que je ne maîtrise pas encore.
Encore une fois Merci, et un autre Merci si vous daigner me montrer avec une loupe ma bêtise, sinon j'aurai peur d'user de la récurrence dans la futur.
Re: Calcul puissance d'une matrice
Bonsoir,
Aymane, il est vrai que tu donnes de plus en plus systématiquement des solutions toutes faites. Je te demanderais donc de ne plus le faire: il est bien plus souhaitable de ne pas donner une solution entièrement rédigée et ce, je puis me le permettre, même si tu estimes personnellement que la discussion est "terminée".
Cordialement
Aymane, il est vrai que tu donnes de plus en plus systématiquement des solutions toutes faites. Je te demanderais donc de ne plus le faire: il est bien plus souhaitable de ne pas donner une solution entièrement rédigée et ce, je puis me le permettre, même si tu estimes personnellement que la discussion est "terminée".
Cordialement
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Calcul puissance d'une matrice
chan79 a écrit:
donc
on peut généraliser le calcul
les valeurs propres sont (a-b) et (a-b+bn)
Pour les nombres sur la diagonale de
Pour les autres nombres:
Je suppose que ça correspond au résultat obtenu avec l'autre méthode.
Modifié en dernier par chan79 le 19 Sep 2016, 21:10, modifié 1 fois.
Re: Calcul puissance d'une matrice
Bonsoir tout le monde,
@aymanemaysae,
Quand j'ai donné ma réponse, je me suis dit "j'ai donné trop d'indications, je n'avais pas à parler du binôme de Newton", car je voulais laisser Maths-ForumR un peu de travail, car dans son message il demandait juste une indication pour débloquer la situation.
Je sais que tu n'es pas de mauvaise foie, j'apprécie tes démonstrations rigoureuses et en plus tu es un adepte de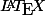 . Ça m'arrive de rédiger comme tu le fais (j'aime bien aussi) mais généralement quand toutes les idées sont présentes dans les messages de façons disparates et qu'il faut tout regrouper pour tout synthétiser.
. Ça m'arrive de rédiger comme tu le fais (j'aime bien aussi) mais généralement quand toutes les idées sont présentes dans les messages de façons disparates et qu'il faut tout regrouper pour tout synthétiser.
Je te souhaite bonne continuation et des message comme celui de Ben314 sont aussi les bienvenus pour recadrer les choses.
@aymanemaysae,
Quand j'ai donné ma réponse, je me suis dit "j'ai donné trop d'indications, je n'avais pas à parler du binôme de Newton", car je voulais laisser Maths-ForumR un peu de travail, car dans son message il demandait juste une indication pour débloquer la situation.
Je sais que tu n'es pas de mauvaise foie, j'apprécie tes démonstrations rigoureuses et en plus tu es un adepte de
Je te souhaite bonne continuation et des message comme celui de Ben314 sont aussi les bienvenus pour recadrer les choses.
Re: Calcul puissance d'une matrice
Bonsoir !
Autre idée : à partir deI+bB,\;B^2=nB) on a
on a
^2I+b^2nB+2b(a-b)B=(a-b)^2I+(nb+2(a-b))bB=(a-b)^2I+(nb+2(a-b))(A-(a-b)I))
d'où=x^2-(nb+2(a-b))x+(a-b)(a-b+nb)) polynôme annulateur de
polynôme annulateur de  .
.
Pour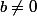 ce polynôme est scindé à racines distinctes
ce polynôme est scindé à racines distinctes  (A est alors diagonalisable)
(A est alors diagonalisable)
Et la division euclidienneP(X)+uX+v) permet, par calcul de
permet, par calcul de 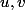 (en utilisant les racines connues de
(en utilisant les racines connues de  ) d'obtenir
) d'obtenir 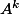 .
.
Pour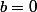 il y a moins de calculs.
il y a moins de calculs.
Autre idée : à partir de
d'où
Pour
Et la division euclidienne
Pour
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
