Calcul de probabilités
24 messages
- Page 1 sur 2 - 1, 2
calcul de probabilités
bonjour a tous je viens vous voir afin que vous me donniez un petit coup de main pour un exercice de probabilité que je n'arrive pas a resoudre.voici l'enoncé:
On place dans une urne U1 3boules blanches et 2 boules noires.
On place dans une urne U2 2 boules blanches et 3 boules noires.
Le jeu consiste a tirer simultanement 2 boules de chaques urnes.
Les tirages sont equiprobables.
On note X la variable aleatoire egale au nombre de boules blanches obtenues a chaque tirage.
Determiner la loi de X et son esperance.
je sais que X peut prendre les valeurs 0,1,2,3 ou 4 mais je n'arrive pas a calculer les probabilités et du coup je ne peux pas calculer l'esperance.Faut il utiliser des combinaisons, des arrangements ou autre chose?
merci d'avance. (c'est pour lundi)
On place dans une urne U1 3boules blanches et 2 boules noires.
On place dans une urne U2 2 boules blanches et 3 boules noires.
Le jeu consiste a tirer simultanement 2 boules de chaques urnes.
Les tirages sont equiprobables.
On note X la variable aleatoire egale au nombre de boules blanches obtenues a chaque tirage.
Determiner la loi de X et son esperance.
je sais que X peut prendre les valeurs 0,1,2,3 ou 4 mais je n'arrive pas a calculer les probabilités et du coup je ne peux pas calculer l'esperance.Faut il utiliser des combinaisons, des arrangements ou autre chose?
merci d'avance. (c'est pour lundi)
Si tu ne veux tirer aucune boule blanche, alors tu dois tirer les deux noires de  .
.
La première est noire, tu as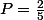
Il reste trois blanches et une noire, pour tirer la deuxième noire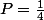
Et dans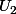 il faut tirer deux boules noires sur les trois.
il faut tirer deux boules noires sur les trois.
Le premier tirage doit être noir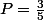
Le deuxième il reste deux noire et deux blanches donc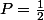
On multiplie toutes les probabilités pour avoir la probabilité totale de n'avoir aucune boule blanche.
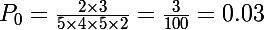
La première est noire, tu as
Il reste trois blanches et une noire, pour tirer la deuxième noire
Et dans
Le premier tirage doit être noir
Le deuxième il reste deux noire et deux blanches donc
On multiplie toutes les probabilités pour avoir la probabilité totale de n'avoir aucune boule blanche.
merci beaucoup je pensais qu'il fallait utiliser des combinaisons.par contre pour avoir 1 boules blanches, ca se complique est ce bon?
1er cas:1 blanche dans U1
il faut donc 1 blanche et 1 noire dans U1 et 2 noires dans U2
probabilité=(3/5)*(2/4)*(3/5)*(2/4)=0.09
2eme cas:1 blanche dans U2
il faut donc 2 noires dans U1 et une blanche et une noire dans U2
probabilité=(2/5)*(1/4)*(2/5)*(3/4)=0.03
conclusion la probabilité d'avoir une blache est de:0.09+0.03=0.12
1er cas:1 blanche dans U1
il faut donc 1 blanche et 1 noire dans U1 et 2 noires dans U2
probabilité=(3/5)*(2/4)*(3/5)*(2/4)=0.09
2eme cas:1 blanche dans U2
il faut donc 2 noires dans U1 et une blanche et une noire dans U2
probabilité=(2/5)*(1/4)*(2/5)*(3/4)=0.03
conclusion la probabilité d'avoir une blache est de:0.09+0.03=0.12
Pour deux boules blanches:
- Deux boules blanches dans et deux noires dans
et deux noires dans 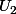 :
:
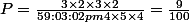
ou
- Deux boules blanches dans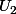 et deux boules noires dans
et deux boules noires dans  :
:
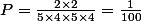
ou
- Une blanche et une noire dans chacune des deux urnes:
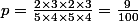
Et comme tu as quatre combinaisons possibles (NBNB, NBBN, BNBN, BNNB), tu multiplies la probabilité par quatre.
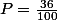
La probabilité totale est égale à la somme de ces trois probabilités:
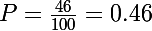
- Deux boules blanches dans
ou
- Deux boules blanches dans
ou
- Une blanche et une noire dans chacune des deux urnes:
Et comme tu as quatre combinaisons possibles (NBNB, NBBN, BNBN, BNNB), tu multiplies la probabilité par quatre.
La probabilité totale est égale à la somme de ces trois probabilités:
encore merci grace a cela j'ai reussi a calculer l'esperance mathematique qui est egale a 2, cela signifie donc que si l'on repete un grand ombre de fois le tirage, on tirera en moyenne 2 boules blanches.
je te remercie vraiment car je suis pas couché avec ces exos.je vais attaquer la suite:
le joueur verse 2 euros en debut de partie et recoit x euros a chaque boule tirée.on appelle Y la variable aleatoire egale au benefice du joueur.
-determiner en fonction de x les valeurs prises par Y
-determiner la loi de probabilité de Y
-determiner le reel x pour que le jeu soit equitable
je vais chercher de mon coté mais si tu as 2 minutes (je pense que c'est le temps que tu vas mettre pour faire cela lol) on pourra comparer les resultats
je te remercie vraiment car je suis pas couché avec ces exos.je vais attaquer la suite:
le joueur verse 2 euros en debut de partie et recoit x euros a chaque boule tirée.on appelle Y la variable aleatoire egale au benefice du joueur.
-determiner en fonction de x les valeurs prises par Y
-determiner la loi de probabilité de Y
-determiner le reel x pour que le jeu soit equitable
je vais chercher de mon coté mais si tu as 2 minutes (je pense que c'est le temps que tu vas mettre pour faire cela lol) on pourra comparer les resultats
euh oui c'est a chaque boule blanche tirée désolé 
moi j'ai trouvé cela:
valeurs prises: -2 ; x-2 ; 2x-2 ; 3x-2 ; 4x-2
loi de proba:
k ///////// -2 /// x-2 /// 2x-2 /// 3x-2 /// 4x-2
p(Y=k)/ 0.03 /// 0.24 /// 0.46 /// 0.24 /// 0.03
reel x pour que le jeu soit equitable:
il faut que E(Y)=2 ce qui nous donne x=2
moi j'ai trouvé cela:
valeurs prises: -2 ; x-2 ; 2x-2 ; 3x-2 ; 4x-2
loi de proba:
k ///////// -2 /// x-2 /// 2x-2 /// 3x-2 /// 4x-2
p(Y=k)/ 0.03 /// 0.24 /// 0.46 /// 0.24 /// 0.03
reel x pour que le jeu soit equitable:
il faut que E(Y)=2 ce qui nous donne x=2
suite:
on suppose x=1 on dit qu'une partie est gagné par le joueur si son gain est strictement positif
determiner la proba que le joueur gagne une partie
je trouve 0.27 (3 et 4 boules blanches)
le joueur fait 10 parties successives les parties sont independantes les unes des autres.on note Z la variable aleatoire egale au nombre de partie gagnées
determiner la loi de Z et ses parametres
je trouve que c'est une loi binomiale de parametre n=10 et p=0.27
calculer la proba que le joueur gagne exactement 4 parties sur les 10
je trouve 0.17 (arrondi a 10-2)
calculer la proba que le joueur gagne au moins 2 parties sur les 10
jee trouve 0.8 (arrondi a 10-2)
on suppose x=1 on dit qu'une partie est gagné par le joueur si son gain est strictement positif
determiner la proba que le joueur gagne une partie
je trouve 0.27 (3 et 4 boules blanches)
le joueur fait 10 parties successives les parties sont independantes les unes des autres.on note Z la variable aleatoire egale au nombre de partie gagnées
determiner la loi de Z et ses parametres
je trouve que c'est une loi binomiale de parametre n=10 et p=0.27
calculer la proba que le joueur gagne exactement 4 parties sur les 10
je trouve 0.17 (arrondi a 10-2)
calculer la proba que le joueur gagne au moins 2 parties sur les 10
jee trouve 0.8 (arrondi a 10-2)
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
