Calcul de primitives - Méthodes.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2011, 19:40
par Deluxor » 14 Nov 2011, 19:40
Bonsoir,
Je manque de méthode pour le calcul de primitives, pouvez-vous me donner des indications pour calculer les primitives suivantes?
a)
 = \frac{x^2 + 3}{x^2 - x + 5})
b)
 = \frac{x+2}{(x+8) sqrt{x+4}})
c)
 = \frac{arctanx}{x^2})
d)
 = \frac{1}{2 + cosx})
D'avance merci,
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 15 Nov 2011, 04:46
par fibonacci » 15 Nov 2011, 04:46
Bonjour;
se ramener à des primitives usuelles
 = \frac{x^2 + 3}{x^2 - x + 5}={{x-2}\over{x^2-x+5}}+1)
=\frac{x+2}{(x+8) sqrt{x+4}}= \frac{x+2+6-6}{(x+8) sqrt{x+4}}=\frac{1}{ sqrt{x+4}}-\frac{6}{(x+8)sqrt{x+4}})
)
ipp en posant
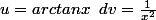
)
en posant
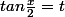
d'où
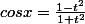
-
Black Jack
 par Black Jack » 15 Nov 2011, 11:47
par Black Jack » 15 Nov 2011, 11:47
Alternative :
Pour g(x)
Le changement de variable x+4 = 4t² amène à : 4.S dt - 6.S 1/(t²+1) dt
:zen:
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 21 Nov 2011, 19:09
par Deluxor » 21 Nov 2011, 19:09
fibonacci a écrit:Bonjour;
se ramener à des primitives usuelles
 = \frac{x^2 + 3}{x^2 - x + 5}={{x-2}\over{x^2-x+5}}+1)
=\frac{x+2}{(x+8) sqrt{x+4}}= \frac{x+2+6-6}{(x+8) sqrt{x+4}}=\frac{1}{ sqrt{x+4}}-\frac{6}{(x+8)sqrt{x+4}})
)
ipp en posant
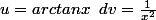
)
en posant
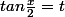
d'où
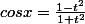
Pour

, je ne comprends pas quelle est la primitive usuelle : on n'a pas la forme
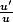
.
Pour g, je reconnais la forme

mais je ne reconnais pas la forme de
 sqrt{x+4} })
Pour h, j'arrive à :
 dx =\frac{-arctan(b)}{b} + \frac{arctan(a)}{a} + \bigint_{a}^{b} \frac{1}{x^3 + x} dx)
Merci d'avance,
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 21 Nov 2011, 19:53
par fibonacci » 21 Nov 2011, 19:53
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Nov 2011, 07:43
par fibonacci » 22 Nov 2011, 07:43
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Nov 2011, 08:01
par fibonacci » 22 Nov 2011, 08:01
Pour k(x)
devient

-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Nov 2011, 09:49
par fibonacci » 22 Nov 2011, 09:49
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 23 Nov 2011, 19:01
par Deluxor » 23 Nov 2011, 19:01
fibonacci a écrit:-3}{2(x^2-x+5)})
Merci mais je ne vois pas comment poursuivre :
On arrive à :

Et je ne vois pas comment calculer la dernière primitive...
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 23 Nov 2011, 19:23
par GagaMaths » 23 Nov 2011, 19:23
pr la derniere, je crois qu'il faut mettre 5 en facteur, et tu te ramènes à une intégrale du type 1 / (1 + X²) en mettant sous une forme canonique...
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 23 Nov 2011, 19:29
par Deluxor » 23 Nov 2011, 19:29
GagaMaths a écrit:pr la derniere, je crois qu'il faut mettre 5 en facteur, et tu te ramènes à une intégrale du type 1 / (1 + X²) en mettant sous une forme canonique...
} dx)
c'est ce que tu me conseilles?
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 23 Nov 2011, 19:39
par fibonacci » 23 Nov 2011, 19:39
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 23 Nov 2011, 19:55
par Deluxor » 23 Nov 2011, 19:55
Merci !
On arrive à :
 dx = x + \frac{1}{2} ln(|x^2-x+5|) + \bigint \frac{-3}{2X^2 + \frac{19}{2}} dx)
C'est ça? Comment poursuivre?
[CENTER]------------------------------------[/CENTER]
Aussi :
Est-ce juste :
 dx = 4t - 6 arctan(t) = 2 sqrt{x+4} - 6 arctan( \frac{ sqrt{x+4} }{2})
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 23 Nov 2011, 20:14
par Deluxor » 23 Nov 2011, 20:14
Merci !
On arrive à :
 dx = x + \frac{1}{2} ln(|x^2-x+5|) + \bigint \frac{-3}{2X^2 + \frac{19}{2}} dx)
C'est ça? Comment poursuivre?
[CENTER]------------------------------------[/CENTER]
Aussi :
Est-ce juste :
 dx = 4t - 6 arctan(t) = 2 sqrt{x+4} - 6 arctan( \frac{ sqrt{x+4} }{2})
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 24 Nov 2011, 05:21
par fibonacci » 24 Nov 2011, 05:21
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités