Calcul de Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AntoineRx
- Messages: 4
- Enregistré le: 27 Mar 2019, 20:47
-
 par AntoineRx » 27 Mar 2019, 20:57
par AntoineRx » 27 Mar 2019, 20:57
Bonjour,
Je n'arrive pas à calculer la primitive de la fonction suivante :
}{1+\sin(x)^2})
J'ai déjà essayer de transformer le tan(x) afin d'appliquer un changement de variable mais sans succès, quelqu'un aurait-il la solution ?
-
mathelot
 par mathelot » 27 Mar 2019, 21:14
par mathelot » 27 Mar 2019, 21:14
bonsoir,
}dx)
)}dx)
on pose
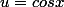
})
})
puis décomposition en éléments simples
il existe A,B,C réels tels que
}=\dfrac{A}{u}+\dfrac{B}{u-\sqrt{2}}++\dfrac{C}{u+\sqrt{2}})
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Mar 2019, 22:29
par Pisigma » 27 Mar 2019, 22:29
Bonsoir,
autre piste: remplacer
)
=\dfrac{tan^2(x)}{1+tan^2(x)})
[1+tan^2(x)]}{1+2~ tan^2(x)}dx)
on pose
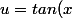)

....
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 27 Mar 2019, 23:03
par tournesol » 27 Mar 2019, 23:03
-
AntoineRx
- Messages: 4
- Enregistré le: 27 Mar 2019, 20:47
-
 par AntoineRx » 28 Mar 2019, 09:29
par AntoineRx » 28 Mar 2019, 09:29
Merci beaucoup à tout le monde !
-
mathelot
 par mathelot » 30 Mar 2019, 12:05
par mathelot » 30 Mar 2019, 12:05
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités