Calcul de longueur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aispor
- Membre Relatif
- Messages: 257
- Enregistré le: 04 Mar 2018, 11:18
-
 par Aispor » 11 Fév 2019, 22:34
par Aispor » 11 Fév 2019, 22:34
Bonjour,
je dois calculer la longueur de deux courbes :
 = (sin(2t),tan(3t)))
disons sur

 = (\frac{1}{t} +ln(2+t), t+ \frac{1}{t}))
sur

L'énoncé nous dit de le calculer (éventuellement avec un calculatrice ou un ordinateur)
La longueur étant défini comme l'intégrale (sur le domaine ci-dessus) de la norme de la dérivée de la courbe... Les choses me paraissent assez horribles x) ... est-il possible de le faire à la main ?
Merci beaucoup

-
aviateur
 par aviateur » 12 Fév 2019, 00:10
par aviateur » 12 Fév 2019, 00:10
Bonjour
A la main pas de problème. Tes courbes sont de longueurs infinies.
C'est simple dès que tu as une branche infinie ....
Il faudrait des morceaux de courbe
Ensuite très souvent le calculs exact n'est pas possible seul un calcul numérique est faisable
Pas étonnant qu'on demande d'utiliser la calculatrice
-
Aispor
- Membre Relatif
- Messages: 257
- Enregistré le: 04 Mar 2018, 11:18
-
 par Aispor » 12 Fév 2019, 07:55
par Aispor » 12 Fév 2019, 07:55
Dac merci

-
aviateur
 par aviateur » 12 Fév 2019, 18:35
par aviateur » 12 Fév 2019, 18:35
Tu as une branche infinie la longueur est infinie.
D'ailleurs en
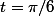
,
||\sim cste/(\pi/6-t))
ce qui fait que l'intégrale est divergente.
-
aviateur
 par aviateur » 12 Fév 2019, 18:37
par aviateur » 12 Fév 2019, 18:37
J'ai rêvé ou quoi. Tu as supprimé un message?
-
Aispor
- Membre Relatif
- Messages: 257
- Enregistré le: 04 Mar 2018, 11:18
-
 par Aispor » 12 Fév 2019, 18:37
par Aispor » 12 Fév 2019, 18:37
Oui pardon l'argument sur tan(.) N'était pas bon ^^ excuse moi j'ai du effacer le message avant que tu répondes :p
Merci

-
Aispor
- Membre Relatif
- Messages: 257
- Enregistré le: 04 Mar 2018, 11:18
-
 par Aispor » 12 Fév 2019, 18:38
par Aispor » 12 Fév 2019, 18:38
J'étais allé voir la primitive de tan(.) Entre temps x)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
