Calcul de la loi de X+Y

[Carlamathsma]

Bonjour, j’ai un exercice à faire en Proba dans lequel je dois calculer la loi de Z = X+Y tel que X et Y sont des variables aléatoires de loi uniforme sur [0,1].
J’ai la fonction de répartition de Z :

Si x<0 alors elle vaut 0
Si 0<=x<1 elle vaut x^2/2
Si 1<=x<2 elle vaut 2x - (x^2)/2 - 1
Si x >= 2 elle vaut 1

Le seul problème c’est que j’arrive pas à trouver le résultat pour xE[1,2] quand je fais le calcul et je ne sais pas comment faire. Quelqu’un pourrait m’aider?

[LB2]

Bonjour,

tu dis que tu dois calculer la loi de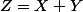 , mais tu as déjà la fonction de répartition . Donc tu connais la loi de Z, non?
Si tu cherches la densité de probabilité de Z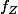 , il suffit de dériver sa fonction de répartition.
Tu sais normalement dériver un polynôme du second degré (programme du lycée).
Vérifie bien que la fonction de densité et toujours positive, et d'intégrale totale 1.

Il existe une formule pour obtenir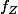 directement sans passer par la fonction de répartition. On l'appelle produit de convolution (intégrale qui se calcule, et fait intervenir 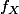et 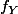). On trouve évidemment le même résultat.

[GaBuZoMeu]

La question a été posée récemment sur un autre forum, et on y a indiqué un moyen clair de calculer la fonction de répartition.
On se place dans le plan. L'axe des abscisses pour , celui des ordonnées pour . Un événement concernant les variables aléatoires réelles et s'identifie à une partie de ce plan. Par exemple l'événement est le demi-plan décrit par cette inégalité.
On dessine le carré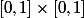 . Puisque les variables et sont indépendantes et de loi uniforme sur , la probabilité d'un événement est l'aire de l'intersection de cet événement avec le carré.
Pour calculer la probabilité de avec tu peux calculer l'aire de la portion du carré sous la droite 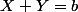. Je pense que tu peux y arriver !

[Carlamathsma]

Le problème dans mon cas c’est juste que je sais ce que vaut la fonction de répartition quand tE(1,2) mais quand j’essaye de la retrouver par le calcul je ne tombe pas sur le même résultat....
Je fait
l’integrale de 1 a t de l’integrale de 1 à t-x dy dx

Concernant le carré je ne vois pas trop comment faire on ne l’a jamais vu en cours