Si non, peut-on y arriver en supposant
Calcul et loi binomiale négative
3 messages
- Page 1 sur 1
Calcul et loi binomiale négative
par PointFix » 07 Fév 2014, 14:35
Soit 
tels que 
, et soit 
. Peut-on démontrer que
^{k-q} \: \: < \: \: \: \sum_{i=nq}^{nk+n-1} \left[ {{i-1} \choose {nq-1}} p^{nq} (1-p)^{i-nq} \right] \: ?)
Si non, peut-on y arriver en supposant
Si non, peut-on y arriver en supposant
par Frede » 08 Fév 2014, 13:23
J'essaie d'y voir un peu clair, tes notations ne sont pas standard.
La partie gauche de ton inéquation représente la probabilité de voir passer q faces avant d'avoir p piles en lançant k fois une pièce de monnaie truquée ayant une probabilité q de sortir un pile et une probabilité (1-q) de sortir un face.
La partie droite représente un peu la même chose mais q est remplacé par nq et k est remplacé par i. Ces deux remplacements veulent dire que la probabilité d'un échec (c'est-à-dire d'un face) est devenue n fois plus grande. Donc la probilité d'un échec est multipliée par n mais en compensation, on multiplie le nombre de lancers par n.
La partie droite représente la somme des probabilités de voir passer nq faces avant de sortir i piles en lançant nk+n fois la pièce de monnaie, la somme se faisant depuis i=nq+1 jusqu'à i=nk+n.
Pour se fixer les idéees, donnons-nous des valeurs; Dans la partie gauche, on lance 5 fois (k=5) une pièce de monnaie ayant une probabilité p=0.30 de sortir un pile et une probabilité q=0.7 de sortir un face et l'expression représente la probabilité de sortir par exemple 3 (ou k-q) faces avant d'obtenir 2 piles (q=2)
Dans la partie droite, le nombre de lancers varie de nq (n peut être quelconque, imaginons que n=10) donc le nombre de lancers va de 70 à nq+n-1 soit 59 et chaque fois on veut obtenir 30 piles avant d'obtenir (i-30) faces.
Mais là, je décroche car i doit être un nombre entier et nq ne l'est pas forcément. q est un nombre décimal, ici, je l'ai supposé égal à 0,7 et si n=2, ça donne i=1,4 ce qui est absurde.
Pourrais-tu vérifier s'il n'y a pas une erreur dans la formule ?
La partie gauche de ton inéquation représente la probabilité de voir passer q faces avant d'avoir p piles en lançant k fois une pièce de monnaie truquée ayant une probabilité q de sortir un pile et une probabilité (1-q) de sortir un face.
La partie droite représente un peu la même chose mais q est remplacé par nq et k est remplacé par i. Ces deux remplacements veulent dire que la probabilité d'un échec (c'est-à-dire d'un face) est devenue n fois plus grande. Donc la probilité d'un échec est multipliée par n mais en compensation, on multiplie le nombre de lancers par n.
La partie droite représente la somme des probabilités de voir passer nq faces avant de sortir i piles en lançant nk+n fois la pièce de monnaie, la somme se faisant depuis i=nq+1 jusqu'à i=nk+n.
Pour se fixer les idéees, donnons-nous des valeurs; Dans la partie gauche, on lance 5 fois (k=5) une pièce de monnaie ayant une probabilité p=0.30 de sortir un pile et une probabilité q=0.7 de sortir un face et l'expression représente la probabilité de sortir par exemple 3 (ou k-q) faces avant d'obtenir 2 piles (q=2)
Dans la partie droite, le nombre de lancers varie de nq (n peut être quelconque, imaginons que n=10) donc le nombre de lancers va de 70 à nq+n-1 soit 59 et chaque fois on veut obtenir 30 piles avant d'obtenir (i-30) faces.
Mais là, je décroche car i doit être un nombre entier et nq ne l'est pas forcément. q est un nombre décimal, ici, je l'ai supposé égal à 0,7 et si n=2, ça donne i=1,4 ce qui est absurde.
Pourrais-tu vérifier s'il n'y a pas une erreur dans la formule ?
par Ben314 » 10 Fév 2014, 11:58
Salut,
Si on part du résultat classique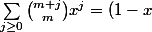^{-(m+1)}\)
(pour 
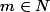et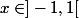 
) on a
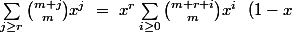^{-(m+1)}-{m+r \choose m}x^r(1-x)^{-(m+r+1)})
Si on regarde ton terme de droite on a :
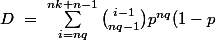^{i-nq}\ <br />=\ p^{nq} \sum_{j=0}^{nk-nq+n-1} {{nq-1+j} \choose {nq-1}} (1-p)^j)
et en appliquant l'inégalité çi dessus, on trouve que
^{nk-nq+n}p^{-(nk+n)}\Big)\ <br />=\ 1-{nk+n-1\choose nq-1} \Big(\frac{1-p}{p}\Big)^{n(k-q+1)})
Mais je sais pas si ça peut t'être utile vu que ce n'est pas trés façile à comparer avec ton terme de gauche...
Si on part du résultat classique
Si on regarde ton terme de droite on a :
et en appliquant l'inégalité çi dessus, on trouve que
Mais je sais pas si ça peut t'être utile vu que ce n'est pas trés façile à comparer avec ton terme de gauche...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :