Calcul de limite d'une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
martin212
- Messages: 5
- Enregistré le: 06 Jan 2008, 11:34
-
 par martin212 » 04 Aoû 2013, 10:08
par martin212 » 04 Aoû 2013, 10:08
Bonjour,
Je dois démontrer que
 = -1)
.
Les outils que je peux utiliser sont les outils usuels de calcul de limites, théorème de comparaison, développement limité, etc. (mais pas la règle de l'Hospital) et pourtant après de multiples tentatives je ne trouve pas ...
Merci d'avance.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 04 Aoû 2013, 10:31
par jlb » 04 Aoû 2013, 10:31
Bonjour, essaie de faire apparaître le nombre dérivé pour exp en 0, comme le quotient - 1/(1+x) tend vers 0 en l'infini, cela fonctionne bien.
[un dl donne encore plus facilement la solution!!!]
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Aoû 2013, 13:10
par deltab » 04 Aoû 2013, 13:10
Bonjour.
Si on ne peut pas utiliser directement la règle de l'Hôpital, il n'est pas interdit d'utiliser le principe c.à.d. faire apparaître des termes dont la limite est par définition la dérivée d'une fonction en un point donné.
C'est l'idée proposée par Jib sans parler de la règle de l'Hôpital.
En développant cette idée, les calculs vont devenir simples. (Je viens de les faire)
-
martin212
- Messages: 5
- Enregistré le: 06 Jan 2008, 11:34
-
 par martin212 » 06 Aoû 2013, 11:51
par martin212 » 06 Aoû 2013, 11:51
Bonjour, merci pour vos réponses, alors je n'ai pas bien compris les histoires de ne pas appliquer la règle mais le principe ... donc j'ai essayé avec un D.L., voilà ce que ça donne. Est-ce que la "rédaction" est correcte ?
)
D.L. de

avec
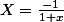
en 0 à l'ordre 1 :
)
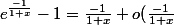={\frac{-1}{x}}+o({\frac{1}{x}}))
Donc,
=\lim_{x\to + \infty} x \cdot \frac{-1}{x} = -1)
Merci.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Aoû 2013, 14:31
par deltab » 06 Aoû 2013, 14:31
Bonjour.
Je n'ai pas vu d'erreurs dans les calculs que tu as fait.
Pour l'histoire de de la règle de l'Hôpital
Faisons le changement de variables
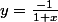
, alors
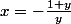
et
=-\frac{1+y}{y}( e^y-1)=-(1+y)\frac{e^y-1}{y})
Quand

, la limite du 1er facteur dans le dernier membres des égalités ne pose pas de problème, le second est une forme indéterminée
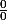
. Mais par définition

'|_{y=0}})
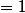
et finalement
= -\lim_{y \to 0^-}(1+y)\frac{e^y-1}{y}=-1)
-
martin212
- Messages: 5
- Enregistré le: 06 Jan 2008, 11:34
-
 par martin212 » 11 Aoû 2013, 07:30
par martin212 » 11 Aoû 2013, 07:30
AAhh ! Merci
deltab, c'est bon j'ai compris !

-
martin212
- Messages: 5
- Enregistré le: 06 Jan 2008, 11:34
-
 par martin212 » 11 Aoû 2013, 07:53
par martin212 » 11 Aoû 2013, 07:53
Encore une petite chose ...
Nous avons montré que :
 = -1)
La suite de la question est la suivante :
Déterminer  et
et  pour que la droite
pour que la droite  d'équation
d'équation  soit asymptote à la courbe
soit asymptote à la courbe 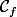 d'équation
d'équation =x e^{\frac{x}{1+x}}) quand
quand  tend vers
tend vers  .
.Voilà où j'en suis arrivé :

est asymptote à
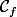
en

si
\right)=0 \Leftrightarrow \lim_{x\to+\infty} x \left( e^{\frac{x}{1+x}} - a\right) = b)
.
Donc on sent bien que c'est de la même forme que ce que l'on vient de montrer mis à part le fait que ce soit

et non

.
Comment conclure ... ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 11 Aoû 2013, 09:18
par jlb » 11 Aoû 2013, 09:18
Bonjour, comme
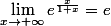
et que
=-e)
alors ton asymptote a pour équation y=ex-e
[tu as un petit dl à faire à nouveau pour trouver la limite ou sinon factoriser par ex pour retrouver la limite précédente, je te laisse faire, bon courage]
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 11 Aoû 2013, 09:19
par emdro » 11 Aoû 2013, 09:19
Bonjour,
Tu peux remarquer que
-1}{1+x}=\cdots-\frac{1}{1+x})
.
Le problème vient du fait que

ne tend pas vers 0 lorsque

tend vers

, donc tu ne peux pas utiliser ton DL d'
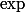
. Voilà pourquoi on est amené à faire cette décomposition. La quantité
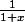
tend bien vers 0 (ce que tu as omis de vérifier en faisant ton DL).
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 11 Aoû 2013, 09:22
par emdro » 11 Aoû 2013, 09:22
Par ailleurs, les formulations :
martin212 a écrit:la courbe
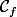
d'équation
=x e^{\frac{x}{1+x}})
et
martin212 a écrit:
est asymptote à
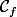
en

si
\right)=0 \Leftrightarrow \lim_{x\to+\infty} x \left( e^{\frac{x}{1+x}} - a\right) = b)
.
sont incorrectes. Je te laisse chercher pourquoi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
