Calcul de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
amed61
- Membre Naturel
- Messages: 20
- Enregistré le: 19 Sep 2012, 20:32
-
par amed61 » 30 Sep 2013, 21:12
chan79 a écrit:J'étais parti un peu autrement (c'est plus long)
On pose
=\fra{1-cos(x)cos(2x)\...\ cos(nx)}{x^2})
donc
cos(2x)\...\ cos(nx) = 1-x^2\,u_n(x))
Ensuite
=\fra{1-cos((n+1)x)\times (1-x^2\,u_n(x))}{x^2})
=\fra{1-cos((n+1)x)+cos((n+1)x)\times x^2\,u_n (x)}{x^2})
=\fra{1-cos((n+1)x)}{x^2}+\fra{cos((n+1)x)\times x^2\,u_n (x)}{x^2})
si
a comme limite
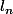
quand x tend vers 0, alors le second quotient a comme limite
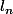
Le premier quotient est égal à
x}{2}\)}{x^2}=\fra{2sin^2\(\fra{(n+1)x}{2}\)}{\(\fra{(n+1)x}{2}\)^2}\times \fra{(n+1)^2}{4})
La limite du premier quotient est donc
^2}{2})
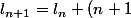^2}{2})
On montre que
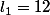
Ensuite, par téléscopage
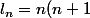(2n+1)}{12})
Bonsoir
C'est une méthode intéressante surtout qu'elle utilise les suites qu'on étudie en première
Merci
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 01 Oct 2013, 13:57
Bj
Une remarque:
la règle de l'hospital (qu'on peut justifier facilement en terminale) permet de conclure très facilement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
