Calcul de limite ( cosinus)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
arthur56000
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Déc 2011, 16:09
-
 par arthur56000 » 23 Déc 2011, 16:21
par arthur56000 » 23 Déc 2011, 16:21
On pose x-> cos²x -1/2*(cos(2x))
Calculer f'(x), que peut-on en déduire?
Merci pour votre aide !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Déc 2011, 16:57
par barbu23 » 23 Déc 2011, 16:57
Salut :
 = - 2 \cos (x) \sin (x) - \frac{1}{2} (- 2 \sin (2x) ) = - 2 \cos (x) \sin (x) + \sin (2x) = 0 $)
Donc :

est "..." ( remplie les pointillés ).
:happy3:
-
arthur56000
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Déc 2011, 16:09
-
 par arthur56000 » 23 Déc 2011, 17:13
par arthur56000 » 23 Déc 2011, 17:13
Je ne vois pas qu'est ce qu'on peut en déduire, j'avais trouvé la même dérivé aussi. Merci.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Déc 2011, 17:15
par barbu23 » 23 Déc 2011, 17:15

est donc constante. :happy3:
-
arthur56000
- Membre Naturel
- Messages: 13
- Enregistré le: 23 Déc 2011, 16:09
-
 par arthur56000 » 23 Déc 2011, 17:34
par arthur56000 » 23 Déc 2011, 17:34
Merci beaucoup j'étais bloqué. Après dans l'énoncé il me demande en déduire que:
cos²x=1/2*(1+cos(2x))
J'ai commencé comme ceci :
-2cos(x)sin(x)+sin(2x)=0
-2cos(x)sin(x)+2cos(x)sin(x)=0
La je suis bloqué..
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Déc 2011, 18:09
par barbu23 » 23 Déc 2011, 18:09
Non, tu as :
 = \cos^2 (x) - \frac{1}{2} \cos (2x ) = A $)
avec

une constante
à déterminer, car dans la question précédente, on a déduit que

est constante ( i.e. :
 = A $)
pour tout

)
Donc, pour
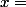
:
 = \cos^2 ( 0 ) - \frac{1}{2} \cos (0 ) = 1 - \frac{1}{2} = \frac{1}{2} $)
Donc, pour tout

:
 = \frac{1}{2} $)
Et tu en déduis maintenant facilement, le résultat.
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
