Calcul de limite avec logarithme (BAC +1)

[Smurfys]

Bonjour, j'ai décidé pendant les vacances, de reprendre un peu les mathématiques, puisque j'ai eu beaucoup de mal durant l'année. J'essaye donc de faire des calculs de limites, mais je pense avoir tout oublié.
Voici l'équation :
Je ne me souviens plus comment faire, mais je crois qu'il faut commencer par la parenthèse, en sachant qu'elle est indéterminée car .
Je vous remercie beaucoup.

[hdci]

Le terme dans le logarithme est peut-être ne forme indéterminée "infini sur infini", mais on sait calculer sa limite très précisément ! et sa limite est 1.

Ceci dit on a donc on se trouve face à une forme indéterminée

Pour résoudre, un moyen est d'utiliser les développements limités. Connaissez-vous le développement limité de au voisinage de 0 ? Si oui, vous avez la réponse en posant .

Sans les développements limités, vous pouvez y arriver en posant
En effet, tend vers 0 quand tend vers l'infini, et alors l'expression que vous obtenez ressemble beaucoup à la définition d'un nombre dérivé d'une certaine fonction en 0.

[Smurfys]

En effet, j'ai vu le développement limité, je ne suis pas sûr de bien m'en souvenir. Mais je ne comprends pas pourquoi on doit l'utiliser ici. Et comment le mettre en place dans une copie. Peut-on dire : On sait que le développement limité de tant vers ... donc ...
Avez-vous une méthode dite "générale" pour résoudre ce genre de calcul de limite ? Car j'aimerai en faire plusieurs, sachant qu'ils deviennent de plus en plus difficiles.

Je vous remercie.

[hdci]

Non, il ne s'agit pas de dire que le développement limité tend vers quoi que ce soit.

Le développement limité c'est une égalité : à l'ordre n, c'est



la sigification de : pour éviter d'écrire avec
Cela représente également un terme négligeable devant (qui est lui-même très petit au voisinage de 0).

L'utilisation du développement limité, c'est qu'on transforme une fonction "à comportement pas bien maîtrisé" en un polynôme : ici quand on divise par x, on voit tout de suite que cela fait 1+ quelque chose avec x en facteur, ce qui permet de calculer facilement la limite quand x->0.

C'est le cas ici : on a un logarithme qui tend vers 0, un entier qui tend vers l'infini, comment résoudre la forme indéterminée : avec le développement limité, le x est en fait 1/n et quand on multiplie par n, il reste 1 plus une somme avec des 1/n, 1/n^2, etc. qui fait 0 quand n tend vers l'infini.

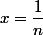
Et ici, il n'est pas besoin de faire un développement limité à l'ordre n : un développement limité à l'ordre 1 suffit : on pose et on obtient


Si gène, on peut remplacer par compte tenu de la définition de

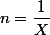
Pour la seconde résolution : l'idée est de transformer l'expression en un truc du genre car quand X tend vers 0, la limite (si elle existe) est . C'est une méthode assez efficace également, ici avec vous obtenez :



Il n'y a plus qu'à dériver en 0.

[Smurfys]

D'accord je comprends mieux merci.
J'ai une autre limite à calculer, la voici :
Vu qu'il y a un "" devant la racine, le calcul n'est pas possible. Je pense qu'il faut chercher avec le développement limité de car si l'on divise la racine par , on obtient , mais le "" devant la racine reste... Je n'ai pas trop d'idée sur la résolution de celle-ci.

En tout cas, merci beaucoup

[hdci]

Effectivement en développement limité.

On peut écrire



Puis
Donc


Il n'y a pus qu'à terminer le calcul.

[LB2]

Bonjour,

dans ce dernier cas, on peut aussi utiliser l'expression conjuguée pour lever l'indétermination en se passant des développements limités.

En effet, en utilisant l'identité remarquable .

Et en factorisant par au dénominateur, on obtient la limite cherchée.

Cordialement

[Black Jack]

Salut,

Pour la question 1 ...

On peut écrire sous la forme lim(n--> +oo) [ln((n+1)/n)/(1/n)], on a une forme indéterminée de la forme 0/0 et on peut donc appliquer la règle du génial Marquis (Lhospital)

= lim(n--> +oo) [(n/(n+1)) * (n-n-1/n²)/ (-1/n²)] = lim(n--> +oo) [n/(n+1)] = 1

[Smurfys]

Super merci beaucoup !