Bonjour,
Pourrais-je avoir une astuce pour calculer explicitement cette intégrale:
f(a,x)=int(exp(-ixt)*1/(a²+t²),t=-infinty..+infinity)
Merci d'avance
Calcul d'intégrale
7 messages
- Page 1 sur 1
salut,
jprends des risques, mais je pense qu'on peut s'en tirer comme ca
 = \bigint_R \frac{1}{a^2+t^2}e^{ -ixt} dt)
Bon, on fait un coup de fractions rationnelles
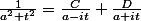
avec C et D des coeffs a déterminer
Ensuite, on separe l'intégrale avec nos deux fractions et on sort les coeff C et D.
On veut alors intégrer
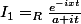
et
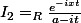
Concernant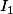 , on remarque que
, on remarque que
 est la transformée de fourier de
est la transformée de fourier de ) et on a envie de faire apparaitre la transformée inverse dans l'intégrande pour dire que ca vaut qqch du genre
et on a envie de faire apparaitre la transformée inverse dans l'intégrande pour dire que ca vaut qqch du genre )
Du coup, on veut faire apparaitre

Jpense qu'on peut alors poser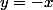
de fait,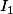 devient alors
devient alors
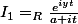
et
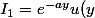 = e^{ ax}u(-x))
Concernant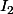
on pose le changement de variable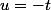 et
et 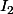 devient alors
devient alors
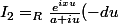)
et on retrouve la même forme qu'avant
Je peux me tromper.
jprends des risques, mais je pense qu'on peut s'en tirer comme ca
Bon, on fait un coup de fractions rationnelles
avec C et D des coeffs a déterminer
Ensuite, on separe l'intégrale avec nos deux fractions et on sort les coeff C et D.
On veut alors intégrer
et
Concernant
Du coup, on veut faire apparaitre
Jpense qu'on peut alors poser
de fait,
et
Concernant
on pose le changement de variable
et on retrouve la même forme qu'avant
Je peux me tromper.
la vie est une fête 
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
