Calcul d'intégral (pas évident)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 22 Nov 2009, 13:43
par sky-mars » 22 Nov 2009, 13:43
Bonjour
Existe-t-il une formule pour calculer ces intégrales s'il vous plait :
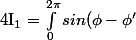 cos(u cos(\phi-\phi')) d\phi')
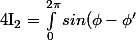 sin(u cos(\phi-\phi')) d\phi')
Sinon y'a un truc que je sais c'est que :
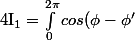 cos(u cos(\phi-\phi')) d\phi' = 0 \forall`\phi)
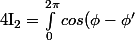 sin(u cos(\phi-\phi')) d\phi' = 2\pi J_1(u))
(étant la fonction de Bessel de 1ère espèce d'ordre 0)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 13:58
par Ben314 » 22 Nov 2009, 13:58
il me semble que t=cos(phi-phi') ; dt=sin(phi-phi') dphi' ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 22 Nov 2009, 14:03
par sky-mars » 22 Nov 2009, 14:03
Bon !
j'ai trouvé la réponse pour ceux qui sont intéressés voici la réponse
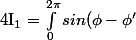 cos(u cos(\phi-\phi')) d\phi')
Je pose :
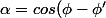)
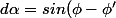 d\phi')
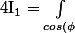}^{cos(\phi)} cos(\alpha u ) d\alpha = 0)
Même raisonnement pour
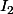
et on trouve aussi
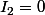
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 22 Nov 2009, 14:03
par sky-mars » 22 Nov 2009, 14:03
exact ben ! je viens de m'en rendre compte ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités