Calcul d'Espérance et de Variance

[RegresseurLineaire]

Bonjour !

J'ai un petit souci de calcul d'Espérance pour une variable aléatoire : On pose et
si t est pair
si t est impair

J'ai lancé une simulation sur R et il semble que l'espérance sera sauf que je n'arrive pas à le prouver sur le papier. Est-ce que quelqu'un a un idée ?

Et du coup j'aurai aussi le souci pour calculer la variance, mais chaque chose en son temps

Merci et bonne journée !

[GaBuZoMeu]

Bonjour,

Je ne vois absolument rien d'aléatoire dans ta définition des . Peux-tu revoir ta question ?

[RegresseurLineaire]

Pour remettre dans le contexte, on cherche à estimer la variance d'une variable aléatoire et je veux montrer que la définition "classique" de l'écart-type est plus imprécise qu'une définition par moyenne mobile .

Pour ça j'ai du coup commencé par calculé les deux sur un échantillon de loi normal centré et réduite (les deux sont quasiment identiques), puis sur un échantillon où la première moitié est de loi normal centré et réduite et la deuxième moitié est de loi normal d'espérance 5 et de variance 1 (là les résultats sont flagrants : sur un changement brutal de moyenne est complètement faux).
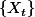
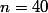
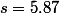
Il me reste à présent à prendre en compte un dernier cas de figure : celui où les données suivent une dérives constante (d'où ma définition de ). Les résultats sont effectivement différents, pour , on obtient et .

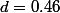
Sauf que pour les comparer il me faudrait la variance théorique, d'où ma question.

(Je sais pas si je suis super clair ^^)

[GaBuZoMeu]

Non, ce n'est absolument pas clair.

Qu'est-ce que tu veux dire par " est complètement faux" ???
Qu'est-ce que tu veux dire par "définition imprécise" ????

Et je répète ma question à laquelle tu n'as absolument pas répondu.

Quand je lis ta définition, je vois , , , etc.; Rien d'aléatoire là-dedans. Quelle serait la variable aléatoire dont tu cherches à calculer l'espérance ???

[RegresseurLineaire]

Qu'est-ce que tu veux dire par " est complètement faux" ???

La variance de l'échantillon est 1, pourtant l'estimateur donne une variance de 2.68

Qu'est-ce que tu veux dire par "définition imprécise" ????

Que dans certains cas on ne pourra pas faire une estimation correcte de , et qu'il faut donc prendre un autre estimateur que

Et je répète ma question à laquelle tu n'as absolument pas répondu.

Quand je lis ta définition, je vois , , , etc.; Rien d'aléatoire là-dedans. Quelle serait la variable aléatoire dont tu cherches à calculer l'espérance ???

Je voudrais calculer la variance de pour pouvoir ensuite la comparer aux valeurs trouvées pour et , sauf que comme tu l'a dit ce n'est pas aléatoire. Je cherche donc à quoi je pourrais comparer mes valeurs

[GaBuZoMeu]

La variance de l'échantillon est 1, pourtant l'estimateur donne une variance de 2.68

C'est un peu n'importe quoi vu que, si j'ai bien compris, la moitié de l'"échantillon" est tiré suivant une loi et l'autre moitié suivant une autre loi. Non ?
L'estimateur dont tu as donné la formule estime l'écart-type pour un échantillon tiré TOUJOURS SUIVANT LA MÊME LOI.

Est-ce que ton problème est le suivant.
Tu as une variable aléatoire et tu prends une suite de réalisations de où les sont indépendantes de même loi que et une fonction (connue ? inconnue ? sur laquelle on a des informations partielles ?).
À partir de là, tu voudrais estimer l'espérance et l'écart-type de ?