[Prépa] Calcul d'équivalent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
NiCKoLaS
- Messages: 7
- Enregistré le: 21 Juil 2015, 15:39
-
 par NiCKoLaS » 21 Juil 2015, 15:51
par NiCKoLaS » 21 Juil 2015, 15:51
Bonjour !
Je bloque sur la question 3 de l'exercice suivant.
Soit
)
la suite définie par :

1- Montrer que la suite est bien définie.
2- Montrer que la suite tend vers 0.
3- En calculer un équivalent
Il semble que

ne soit pas un
)
, mais à part ça, je ne trouve aucun résultat intéressant, même en essayant de chercher "à l'aveugle" quel équivalent pourrait convenir (

etc.).
Des suggestions ?
Merci d'avance.
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 21 Juil 2015, 16:32
par lionel52 » 21 Juil 2015, 16:32
Salut tu as

On pose
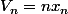
, alors
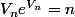
 = ln(n))
et
)
car
)
est négligeable devant

-
NiCKoLaS
- Messages: 7
- Enregistré le: 21 Juil 2015, 15:39
-
 par NiCKoLaS » 22 Juil 2015, 08:56
par NiCKoLaS » 22 Juil 2015, 08:56
Merci bien. (Je me sens très bête !)
Je bloque sur un autre exercice d'équivalent :
Soit

la fonction définie sur
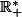
par :
 = \underset{n\to +\infty}{lim} \frac{n^{x}n!}{\prod_{k=0}^n (x+k)})
1- Montrer que

est bien définie
2- Montrer que
=x\Gamma(x))
.
3- Calculer
)
(on pourra utiliser la formule de Stirling).
A la dernière question, je ne vois pas en quoi la formule de Stirling est utile (le problème, pour moi, est plus de calculer un équivalent du bas qu'un équivalent du haut)...
Merci d'avance.
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 22 Juil 2015, 12:21
par lionel52 » 22 Juil 2015, 12:21
Re!
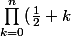<br />= \frac{1}{2^n}\prod_{k = 0}^n (2k+1)<br />= \frac{1}{2^n} 1.3.5.....(2n+1)<br />= \frac{1}{2^n} 1.2.3.4.5.....(2n+1)/(2.4.6....2n))
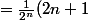!/((2.1)(2.2)....(2.n))<br />= \frac{1}{4^n}(2n+1)!/n!)
-
NiCKoLaS
- Messages: 7
- Enregistré le: 21 Juil 2015, 15:39
-
 par NiCKoLaS » 22 Juil 2015, 14:54
par NiCKoLaS » 22 Juil 2015, 14:54
Au poil, merci.
Bien vu pour la "double factorielle".
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
la suite définie par :

la suite définie par :

la fonction définie sur
par :
est bien définie
.
(on pourra utiliser la formule de Stirling).