Calcul différentielle 2

[marius1986]

Bien le bonjour à vous, j'ai un pb avec la démo d'un théorème,
Voici le théorème:
Soit E, F et G trois espaces vectoriels normés de dimensions finies. Soit f une application de E vers F et g une application de F vers G.
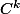
Si f et g sont de classe , alors fog est de classe

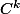
Merci d'avance

[AlexisD]

As-tu essayé par récurrence sur k ?

[klaus2010]

Bonjour,

on a f(x,y)=(B.x-A.y)^T .Q. (B.x-A.y)
ou x,y dans R^n , A,B matrices carrées n*n , Q carrée Symétrique définit positive.

Je veux confirmer grad(f)



grad(f(x,y))=(B .Q.(B.x-A.y) -A. Q. (B.x-A.y))^T


la différentiel de f est-elle la transposé de grad(f) si oui.. comment
on peut le voir comme application linéaire ?

merci en avance ...

[Ben314]

Il me semble qu'il suffit d'écrire la définition de "étre " pour obtenir ce résultat....