Bonjour,
soit

une application

et

l'application:
 = f( \cos(u)+\sin(v), \sin(u)+\cos(v), e^{u-v} ))
.
1) Montrer que

est de classe

2) On suppose que

est differentiable au point
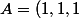)
de

et que sa differentielle en ce point est, en convenant d'identifier, une application lineaire de

dans

avec sa matrice: f '(A) =
1 3 4
2 -1 3
(désolé pour l'ecriture je ne sais pas comment ecrire une matrice)
Déterminer la differentielle de

au point
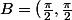)
.
Ce que j'ai pu faire:
1) on a

avec
 = ( \cos(u)+\sin(v), \sin(u)+\cos(v), e^{u-v} ))
je dois montrer que

est differentiable et sa differentiable est continue.
On sait que

est differentiable, donc il reste à montrer que

est differentiable. posons:
+\sin(v))
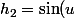+\cos(v))
et

je dirai que les fonctions
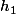
et
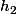
sont differentiables car les fonctions
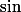
et
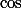
sont de classe

donc la somme sera aussi de
classe

.
Maintenant

on peut dire que
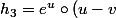)
avec

lineaire donc differentiable et
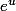
de classe

donc differentiable, on peut donc dire

est differentiable,
on constate que les composantes de

sont differentiables, donc

est diiferentiable.
j'ai du mal à trouver la differentielle de

.
