Bonjour,
ESt-ce que quelqu'un pourrait m'indiquer comment calculer la normale pour les formes géométriques suivantes :
-sphere
-cone
-cube
-cylindre
-paraboloide
Merci
Calcul des normales
5 messages
- Page 1 sur 1
l'équation d'une sphère 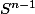 est:
est:
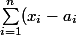^2=R^2)
où) sont les coord. du centre.
sont les coord. du centre.
en différentiant avec un élément)
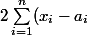h_{i} =0)
donc:
un vecteur normal a pour coord:
) )
)
2) pour le cube, il suffit de prendre un repère lié à un sommet
et de regarder la chose visuellement.
on a des normales sur chaque face sauf sur les arêtes
qui sont simplement
ou leurs opposés selon les faces. La normale n'est pas définie sur les aretes ni sur les sommets.
où
en différentiant avec un élément
donc:
un vecteur normal a pour coord:
2) pour le cube, il suffit de prendre un repère lié à un sommet
et de regarder la chose visuellement.
on a des normales sur chaque face sauf sur les arêtes
qui sont simplement
ou leurs opposés selon les faces. La normale n'est pas définie sur les aretes ni sur les sommets.
tes exemples sont tous ( sauf cube)des quadriques surfaces du second degré
d'équation ax^2 +by^2 cz^2 + dxy+exz+fyz +gx+hy+iz = j (E)
pour avoir l'équation du plan tangent ( et donc d 'un vecteur normal) au point M0(x0,yo,z0) on utilise des règles simples (dédoublement de termes)
dans (E)
on remplace x^2 par xx0 idem pour les autre carrés
on remplace xy par (x0y+xy0)/2 idem pour les autres termes rectangles
on remplace x par (x+x0)/2 ide m pour les autres
exemple la sphère unité
x^2+y^2+z^2 = 1 (S)
équation du plan tangent
xx0 + yy0 +zz0 = 1 vecteur normal : (x0,y0,z0)
d'équation ax^2 +by^2 cz^2 + dxy+exz+fyz +gx+hy+iz = j (E)
pour avoir l'équation du plan tangent ( et donc d 'un vecteur normal) au point M0(x0,yo,z0) on utilise des règles simples (dédoublement de termes)
dans (E)
on remplace x^2 par xx0 idem pour les autre carrés
on remplace xy par (x0y+xy0)/2 idem pour les autres termes rectangles
on remplace x par (x+x0)/2 ide m pour les autres
exemple la sphère unité
x^2+y^2+z^2 = 1 (S)
équation du plan tangent
xx0 + yy0 +zz0 = 1 vecteur normal : (x0,y0,z0)
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
