Calcul des éléments d'intégrations sans passer par la matric

[seriousme]

Bonjour,

dans les intégrales multiples lors d'un changement de variable il est souvent nécessaire de modifier le produit des éléments d'intégrations, la méthode classique consistant à calculer le jacobien de la transformation.

Est-il possible de retrouver les nouveaux éléments d'intégration sans cette méthode ?

Exemple :




Donc :



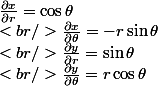
Puis, naïvement, et c'est là que doit se trouver l'erreur :



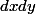
Puis calculer en fonction de à partir de là.

Bien sûr cela ne fonctionne pas du tout .

Où est l'erreur ?

Merci .

[seriousme]

Le problème serait il plus compliqué qu'il n'y paraît ?

[Babe]

dxdy=det(J)drdO
avec J la matrice Jacobienne
det(J)=r
d'où dxdy=rdrdO
en 5s c'est fais avec la matrice jacobienne, pour n'importe quel changement de variable cela marche et c'est rapide

[seriousme]

Oui, bien entendu, mais :
1) comment retrouver ce resultat sans utiliser cet outil ?
2) où se trouve l'erreur dans le raisonnement exposé dans le premier post ?

[Babe]

un moyen facile pour se rapeler le changement sans utiliser la matrice jacobienne
vitesse en coordonées cartesiennes: dxi+dyj+dzk
vitesse en coordonnées cylindriques: dre_r+rdOe_O+dzk

[seriousme]

Merci pour l'astuce .

Mais il doit bien y avoir un moyen simple de retrouver le jacobien sans passer par ce type de procédé .

Le but n'est pas de résoudre un problème pratique, c'est une simple question théorique .
La vraie question sousjacente pourrait être :
d'où vient la notion de jacobien; plus précisément, pourquoi s'exprime t'il ainsi comme déterminant de la matrice jacobienne ?
Comment, par un procédé mathématique simple, sans faire appel à des notions élaborées, sans invoquer des théorèmes dont la démonstration n'est pas évidente, arriver à effectuer un changement de variable sans calculer directement le jacobien ?

La formalisation d'un résultat est une chose, le pourquoi de ce résultat en est une autre .

De même qu'il est possible de retrouver la notion de déterminant en simplifiant et combinant les équations d'un système linéaire, sans passer par les méthodes calculatoires habituelles, il doit bien être possible, en combinant les éléments de base de l'intégrale, de retrouver le résultat .

[Babe]

Merci pour l'astuce .

Mais il doit bien y avoir un moyen simple de retrouver le jacobien sans passer par ce type de procédé .

Le but n'est pas de résoudre un problème pratique, c'est une simple question théorique .
La vraie question sousjacente pourrait être :
d'où vient la notion de jacobien; plus précisément, pourquoi s'exprime t'il ainsi comme déterminant de la matrice jacobienne ?
Comment, par un procédé mathématique simple, sans faire appel à des notions élaborées, sans invoquer des théorèmes dont la démonstration n'est pas évidente, arriver à effectuer un changement de variable sans calculer directement le jacobien ?

La formalisation d'un résultat est une chose, le pourquoi de ce résultat en est une autre .

De même qu'il est possible de retrouver la notion de déterminant en simplifiant et combinant les équations d'un système linéaire, sans passer par les méthodes calculatoires habituelles, il doit bien être possible, en combinant les éléments de base de l'intégrale, de retrouver le résultat .

euh la je ne sais pas , il faut demander a des gens plus qualifier que moi lol