Boule ouverte et fermée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Sep 2017, 20:00
par mehdi-128 » 14 Sep 2017, 20:00
Bonsoir,
On se place dans un espace normé.
Soit
)
(boule fermée de centre a et de rayon r)
Je veux trouver une suite
)
qui appartient à la boule ouverte de centre a et de rayon r
)
et qui converge vers x.
Merci.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 14 Sep 2017, 20:16
par pascal16 » 14 Sep 2017, 20:16
par définition, pour tout n, il existe un boule Bn de rayon 1/n et de centre x telle que l'intersection de ta boule ouverte de Bn soit non vide.
Soit Un, un élément de cette intersection non vide.
Un, n€N est donc une suite d'éléments de la boule ouverte qui converge vers x car ||Un-x||<=1/n.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Sep 2017, 21:14
par mehdi-128 » 14 Sep 2017, 21:14
Rien compris.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Sep 2017, 21:19
par mehdi-128 » 14 Sep 2017, 21:19
Comment montrer que :
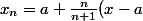 \in B(a,r))
?
On a déjà :
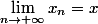

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Sep 2017, 21:23
par Ben314 » 14 Sep 2017, 21:23
mehdi-128 a écrit:Comment montrer que :
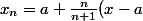 \in B(a,r))
?
Par
définition B(a,r) c'est les x de E tels que ...
Donc pour vérifier que xn est dans B(a,r) il suffit de vérifier que ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 15 Sep 2017, 02:11
par mehdi-128 » 15 Sep 2017, 02:11
Ben314 a écrit: mehdi-128 a écrit:Comment montrer que :
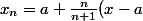 \in B(a,r))
?
Par
définition B(a,r) c'est les x de E tels que ...
Donc pour vérifier que xn est dans B(a,r) il suffit de vérifier que ...
B(a,r) c'est les x de E tels que

Il faut montrer que :

soit :
|| < r)
Or :
|| =\frac{n}{n+1} ||x-a|| < \frac{n}{n+1} r \leq r)
Donc :

et
)


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Sep 2017, 07:28
par Ben314 » 15 Sep 2017, 07:28
C'est presque ça :
mehdi-128 a écrit:Or :
|| =\frac{n}{n+1} ||x-a|| {\red <} \frac{n}{n+1} r {\blue \leq} r)
modulo que :
- En rouge, c'est un "inférieur ou égal" vu que ce qu'on sait concernant x, c'est qu'il est dans la boule
fermée de centre a et de rayon r.
- En bleu, on peut mettre un "strictement inférieur" vu que n<n+1 (strict) et que r>0 (strict).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
?
?