BON de Sym(2,R)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sudille
- Messages: 6
- Enregistré le: 09 Nov 2008, 15:16
-
par Sudille » 10 Avr 2012, 00:13
Salut !
J'essaie de faire un CC de l'an passé pour réviser, mais je reste bloquée à une question...
D'avance merci pour votre aide !
Voici l'énoncé :
Le blocage commence donc à la question 3. Pas de soucis pour donner la première base, mais après ?
... Si vous pouviez me donner au moins les grands axes, merci !
Ce que j'ai testé :
- Matrices 1 et 2 : déterminants qui valent +-1 donc sont déjà normées
- Matrice 3 :
[CENTER]valeurs propres :
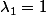
et
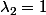
vecteurs propres
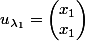
et
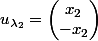
or
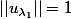
et
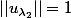
d'où
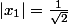
et
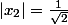
donc
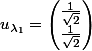
et
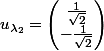
alors
[/CENTER]
... ce qui ne correspond évidemment pas à la solution :help:
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 10 Avr 2012, 17:24
Sudille a écrit:Salut !
J'essaie de faire un CC de l'an passé pour réviser, mais je reste bloquée à une question...
D'avance merci pour votre aide !
Voici l'énoncé :
Le blocage commence donc à la question 3. Pas de soucis pour donner la première base, mais après ?
... Si vous pouviez me donner au moins les grands axes, merci !
Ce que j'ai testé :
- Matrices 1 et 2 : déterminants qui valent +-1 donc sont déjà normées
- Matrice 3 :
[CENTER]valeurs propres :
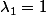
et
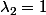
vecteurs propres
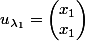
et
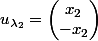
or
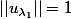
et
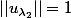
d'où
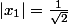
et
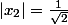
donc
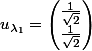
et
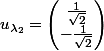
alors
[/CENTER]
... ce qui ne correspond évidemment pas à la solution :help:
La deuxième base est une base orthonormée de Sym(2,R)
Il suffit de vérifier que les 3 matrices sont orthogonales 2 à 2 et de norme 1
cela pour le produit scalaire défini en début de l'exerciceMême remarque pour la dernière base (base de M(2,R))
La base canonique étant aussi orthogonale (tjs pour le même produit scalaire), la matrice de passage de la base canonique vers la base orthonormée ci-dessus sera orthogonale. ce qui est bien vérifié.
-
Sudille
- Messages: 6
- Enregistré le: 09 Nov 2008, 15:16
-
par Sudille » 10 Avr 2012, 18:28
Maxmau a écrit:La deuxième base est une base orthonormée de Sym(2,R)
Il suffit de vérifier que les 3 matrices sont orthogonales 2 à 2 et de norme 1 cela pour le produit scalaire défini en début de l'exercice
Même remarque pour la dernière base (base de M(2,R))
La base canonique étant aussi orthogonale (tjs pour le même produit scalaire), la matrice de passage de la base canonique vers la base orthonormée ci-dessus sera orthogonale. ce qui est bien vérifié.
Bonsoir,
En fait ça je savais, mais je n'avais pas compris que je pouvais réintroduire une nouvelle matrice symétrique dans la base et virer celle qui m'incommodait.
Du coup la suivante a coulé de source. Le seul problème reste de trouver la matrice de passage. Je feuillette les bouquins mais j'ai encore du mal à trouver le rapport --"
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 10 Avr 2012, 19:07
Sudille a écrit:Bonsoir,
En fait ça je savais, mais je n'avais pas compris que je pouvais réintroduire une nouvelle matrice symétrique dans la base et virer celle qui m'incommodait.
Du coup la suivante a coulé de source. Le seul problème reste de trouver la matrice de passage. Je feuillette les bouquins mais j'ai encore du mal à trouver le rapport --"
revois la définition d'une matrice de passage d'une base vers une autre
Exprime chaque matrice de la base d'arrivée comme combinaison linéaire des matrices de la base de départ (base canonique). Les coordonnées de la première matrice donne la première colonne..etc...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
