[MPSI] Bolzano-Weierstrass
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 23 Nov 2006, 06:35
Bonjour,
Je n'arrive pas à faire cet exercice sur les suites :briques: :marteau: . Merci d'avance pour votre aide.
"Soit
_{n \in N})
une suite bornée. Par le Théorème de Bolzano-Weierstrass, on sait que
admet une suite extraite convergente. On suppose dans cet exercice que toutes les suites extraites convergentes de
convergent toujours vers la même limite
.
- On raisonne par l'absurde : on suppose dans cette question que
ne converge pas vers .
¤ Construire une suite extraite de
dont les valeurs sont suffisament éloignées de
.
¤ Construire alors une suite extraite de
convergent vers un réel différent de
."
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 23 Nov 2006, 08:08
Bonjour,
c'est assez simple, utilises la négation de la définition de la convergence...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 23 Nov 2006, 18:34
la définition de
ne converge pas vers
est la suivante :
,
,
,
mais je ne vois pas comment faire avec ceci la première question : :marteau: :mur: :mur:
Par contre pour la deuxième j'ai trouvé quelque-chose
pouvez vous me dire si je répond bien à la question (
car je suis pas tout à fait sur de moi) :
On vient de construire une suite
qui ne converge pas vers
.
Or on sait que
)
est bornée, donc
aussi.
D'après le
théorème de Bolzano-Weierstrass, on peut en extraire une deuxième sous-suite
convergeant vers un réel
.
Pour tout n, on a :
donc par continuité de la fonction valeur absolue, on peut passer à la limite, ce qui nous donne :
en particulier
On a ainsi construit une suite extraite de
convergeant vers un réel
,
différent de .Est-ce correct ??? merci d'avance.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
par alben » 23 Nov 2006, 19:00
Bonsoir,
Le raisonnement le plus naturel est le suivant :
On suppose que la suite ne converge pas vers a. Donc comme tu l'as écrit
,
,
,
Posons
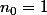
, il existe
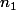
vérifiant l'inégalite
Puis posons
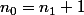
, il existe
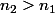
vérifiant l'inégalite
puis avec
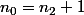
on définit
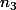
et ainsi de suite
Considérons la sous-suite
)
dont tous les termes vérifient l'inégalite.
D'après le théorème de Bolzano-Weierstrass, on peut en extraire une deuxième sous-suite convergente. Sa limite ne peut être a puisque tous les termes vérifient l'égalité |u-a|>. -> contradiction
Je pense que c'est ce que tu avais en tête
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 23 Nov 2006, 19:36
Merci je comprends, mais je n'arrive pas à le traduire sous la forme :
Montrons par recurrence que ....
Initialisation : ...
Iteration : ....
Conclusion : ....
En fait je ne vois pas comment transposer ce que vous avez marqué ! :help: Pourriez-vous m'aider s'il vous plait ? Merci d'avance.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
