Binome négatif
5 messages
- Page 1 sur 1
Binome négatif
Bonjour mon prof d'ecs ne cesse d'utiliser cette formule sans que je n'y comprenne rien.. Il me parle de dérivée de fonctions géométriques quelqu'un pourrait juste m'en dire plus avec un exemple ??? Merci d'avance
euh,
je me demande,
on peut toujours considérer la série:
=\sum_{n=0}^{+\infty} \, P(X=n) x^{n})
dont le rayon de convergence est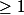
et dans l'intérieur du disque dériver:
= \sum_{n=1}^{+\infty} \, n P(X=n) x^{n-1})
on calcule ainsi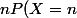) , si l'on a une formule
, si l'on a une formule
explicite de f '.
Les coefficients binomiaux négatifs sont utilisés
dans le développement en série entière de
}^{\alpha}= \sum_{n=0}^{+\infty} \, \frac{\alpha (\alpha -1) \cdots (\alpha - n+1)}{n!} \, x^{n})
pour
je crois qu'on parle alors de coefficients de la série hypergéométrique.
je ne sais si ça répond à la question.
je me demande,
on peut toujours considérer la série:
dont le rayon de convergence est
et dans l'intérieur du disque dériver:
on calcule ainsi
explicite de f '.
Les coefficients binomiaux négatifs sont utilisés
dans le développement en série entière de
pour
je crois qu'on parle alors de coefficients de la série hypergéométrique.
je ne sais si ça répond à la question.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
