Bonjour,
je dois démontrer la bijectivité de l'application F suivante : de E dans E, qui à une suite (xk) associe la suite (yk) telle que y_k=1/(k+1)Somme(j=0 à k, x_j)
Je précise que E est l'ensemble des suites bornées de nombres complexes, et que F est linéaire.
Je crois que pour la surjectivité , c'est bon.
Mais l'injectivité me pose pb : je suis partie de F(x_k)=0 ; je n'arrive pas à prouver que x_k =0, à cause de la somme.
Merci de votre aide.
Bijectivité d'une application de C dans C
6 messages
- Page 1 sur 1
Merci encore pour ta réponse.
Pour la surjectivité, c'est ok.
Pour l'injectivité, je bloque encore. Sur tes conseils, je suis partie sur une récurrence, mais je ne suis pas sure de l'avoir bien construite :
Pour k entier,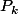 l'assertion "
l'assertion "=\lambda*x_k) entraine
entraine 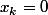 "
"
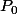 ok
ok
On suppose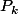 vraie. Il s'agit de prouver
vraie. Il s'agit de prouver 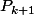
On démarre de=\lambda*x_{k+1})
soit*\Sigma x_j=\lambda*x_{k+1}) (j allant de 0 à k+1) (je ne sais pas bien taper le sigma non plus .... :fan:
(j allant de 0 à k+1) (je ne sais pas bien taper le sigma non plus .... :fan:
je ne vois pas trop comment j'arrive à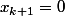 ...?
...?
Merci encore pour le coup de main.
Pour la surjectivité, c'est ok.
Pour l'injectivité, je bloque encore. Sur tes conseils, je suis partie sur une récurrence, mais je ne suis pas sure de l'avoir bien construite :
Pour k entier,
On suppose
On démarre de
soit
je ne vois pas trop comment j'arrive à
Merci encore pour le coup de main.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
