Bijection tangente dérivée arctan

[besten]

Bonjour,

J'ai des soucis pour déterminer la dérivée de la fonction arctan en passant par la bijection.
Si quelqu'un peut m'aiguiller...

Merci

[Anonyme]

Bonjour,

J'ai des soucis pour déterminer la dérivée de la fonction arctan en passant par la bijection.
Si quelqu'un peut m'aiguiller...

Merci

Soit une bijection dérivable et dont la dérivée ne s'annule pas sur .

Alors pour

Prends

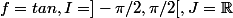
[besten]

Quel est le rapport avec ?
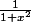
Comment on y arrive ?

[chan79]

Quel est le rapport avec ?
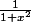
Comment on y arrive ?

y=f(x)=tan x

[Luc]

Quel est le rapport avec ?
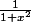
Comment on y arrive ?

Parce que la dérivée de tan c'est 1+tan^2. (cf post de chan)

[besten]

Merci, j'ai compris maintenant !