bonjour tt l monde ,j'ai trouve des difficultes pour montre que :
si on a un bijection de f: N --> N donc lim quand n>+oo de f(n) =+oo
Bijection de N
4 messages
- Page 1 sur 1
yassine-_@hotmail.com a écrit:bonjour tt l monde ,j'ai trouve des difficultes pour montre que :
si on a un bijection de f: N --> N donc lim quand n>+oo de f(n) =+oo
Bonjour,
Regarde par l'absurde :
Il existe A>0 tq pour tout n0 dans N, il existe n>=n0 tq f(n)<A.
Et essaye de faire un dessin de ce que ça veut dire et tu devrais arriver à trouver une contradiction (en raisonnant sur le fait que tu te trouves dans N, la proposition n'est pas vraie dans R par exemple)
Damien
Ce qu'il s'agit de démontrer  \geq A)
sous l'hypothèse f : N --> N bijective.
Au lieu d'un raisonnement par l'absurde (perso, je n'aime pas l'absurde), je propose que de faire une simple récurrence sur l'entier A :
- l'initialisation A=0 est triviale ;
- l'hérédité n'est pas compliquée : si un certain entier A vérifie \geq A) , qu'en est-il pour l'entier A+1 ?
, qu'en est-il pour l'entier A+1 ?
Comme f est bijective, il existe un seul antécédent de A. Et alors, pour tout n à la fois plus grand que
de A. Et alors, pour tout n à la fois plus grand que  et
et 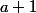 , on a ...
, on a ...
En fait, la preuve à surtout besoin de l'injectivité de f : on démontre ici que si f : N --> N est injective, alors sa limite est infinie.
sous l'hypothèse f : N --> N bijective.
Au lieu d'un raisonnement par l'absurde (perso, je n'aime pas l'absurde), je propose que de faire une simple récurrence sur l'entier A :
- l'initialisation A=0 est triviale ;
- l'hérédité n'est pas compliquée : si un certain entier A vérifie
Comme f est bijective, il existe un seul antécédent
En fait, la preuve à surtout besoin de l'injectivité de f : on démontre ici que si f : N --> N est injective, alors sa limite est infinie.
Ce qu'il s'agit de démontrer  \geq A)
sous l'hypothèse f : N --> N bijective.
Au lieu d'un raisonnement par l'absurde (perso, je n'aime pas l'absurde), je propose de faire une simple récurrence sur l'entier A :
- l'initialisation A=0 est triviale ;
- l'hérédité n'est pas compliquée : si un certain entier A vérifie \geq A) , qu'en est-il pour l'entier A+1 ?
, qu'en est-il pour l'entier A+1 ?
Comme f est bijective, il existe un seul antécédent de A. Et alors, pour tout n à la fois plus grand que
de A. Et alors, pour tout n à la fois plus grand que  et
et 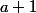 , on a ...
, on a ...
En fait, la preuve a surtout besoin de l'injectivité de f : on démontre ici que si f : N --> N est injective, alors sa limite est infinie.
EDIT, en fait la preuve montre que si f ne prend pas une infinité de fois la même valeur, alors f tend vers l'infini. Et à l'évidence, la réciproque est également vraie. C'est ce que DamX propose de démontrer dans sa proposition de raisonnement par l'absurde, je pense.
sous l'hypothèse f : N --> N bijective.
Au lieu d'un raisonnement par l'absurde (perso, je n'aime pas l'absurde), je propose de faire une simple récurrence sur l'entier A :
- l'initialisation A=0 est triviale ;
- l'hérédité n'est pas compliquée : si un certain entier A vérifie
Comme f est bijective, il existe un seul antécédent
En fait, la preuve a surtout besoin de l'injectivité de f : on démontre ici que si f : N --> N est injective, alors sa limite est infinie.
EDIT, en fait la preuve montre que si f ne prend pas une infinité de fois la même valeur, alors f tend vers l'infini. Et à l'évidence, la réciproque est également vraie. C'est ce que DamX propose de démontrer dans sa proposition de raisonnement par l'absurde, je pense.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
