Bienaymé-Tchebychev

par **les TPEistes** » 27 Avr 2009, 20:50

Bonsoir ! Cet exercice me pose un problème. Si quelqu'un veut s'y pencher et m'aider à comprendre comment le résoudre...

Soit

une suite de réels à valeurs dans

et

une suite de v.a.r. indépendantes telle que

suit une loi de Bernoulli de paramètre

.

Soient

,

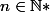
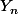
et

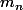
définis par :

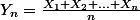
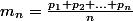
1/ Montrer que, pour tout alpha strictement positif :

2/ Montrer que si

est une suite de limite

, alors pour tout alpha strictement positif :

Merci de m'avoir lu

par **nuage** » 28 Avr 2009, 07:28

Salut,
on peut commencer par majorer la variance de chaque

par 1 (c'est trivial) ou par

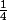
(c'est très facile).
Comme

on a une majoration de

.
Reste alors à utiliser l'inégalité de Bienaymé-Tchebychev.

par **john32** » 28 Avr 2009, 08:04

D'accord avec toi nuage !
Par contre j'avoue ne pas saisir l'enonce de la 2eme question. Ne s'agirait il pas plutot d'un m au lieu d'un mn ? :hein: