BEZIER et equation paramétriques

[jass73110]

Bonjour, je voudrais un peu d'aide, j'ai un petit problème à résoudre pour ma copine à qui je fais le prof de math et jusque là j'avais plutot bien réussite mais je fais face à se que l'on nomme un problème!
J'ai passé mon BTS il y avait un ti peu plus de 10 ans.....
je vous donne l'énoncé:

Exemple de courbe de BEZIER définie par points de définition et polynomes de BERSTEIN.

Dans un repère orthonormal (O,i,j) d'unité graphique 2 centimètre, on donne les points suivants par leurs coordonnées:
A(1,1) B(3,2) C(4,1)
Le but de l'exercice est de déterminer et de tracer une courbe possédant les propriétés suivantes:
- elle passe par les points A B et C
-elle admet le vecteur AB pour vecteur directeur de la tangente à la courbe au point A
-elle admet le vecteur BC pour vecteur directeur de la tangente à la courbe au point C

Pour tout nombre t d'intervalle [0,1], soit M le point défini par:

OM=(1-t)² OA+2t(1-t) OB+t² OC

(Excusez moi pour les vecteurs, je ne peux pas mettre de fleche sur OA ou OB etc........

1) Calculer en fonction de t les coordonnées x et y du point M!

alors ca c'est bon, j'ai trouvé le résultat!
j'ai remplacer dans l'équation et je trouve
je trouve
x=-t²+4t+1 et
y=-2t²+2t+1 (je ne met pas le détaille car c'est long et je sais comment faire, c'est pas là ou est mon problème!! lol)

2) on considère les fonctions f et g définies sur l'intervalle [0,1] par:
f(t)=-t²+4t+1 et g(t)=-2t²+2t+1
Etudier les variations des fonctions f et g sur [0,1] et rassemblez les dans un tableau unique.

Là non plus je ne met pas se que je trouve car je connais la réponse, par contre c'est après. Je vous donne quand meme l'exercise dans sa globalité pour que vous puissiez bien voir)

3) on note T la courbe dans le repère orthonormal (O,i,j) dont un systeme d'équations paramétriques est:
x=f(t)
y=g(t)
ou t appartient à [0,1]
a) montrer que le vecteur AB est un vecteur directeur de la tangente à la courbe T au point Aet que le vecteur BC est un vecteur directeur de la tangente à la courbe T au point C!

:mur: alors là je ne sais pas comment faire! je sais calculer une tangente sur une courbe classique genr parabole, mais là, une courbe faite de deux courbes!!!
Merci de me donner l'explication. Est ce que c'est du genre Y-X!
ensuite
b) determinerun vecteur directeur de la tangente à la courbe T au point S obtenu pour t=1/2
c)tracer...

Merci si quelqu'un connais la réponse à la 3a et 3b de me donner le résultat!!
merci bien!
JASS

[nuage]

Salut,
Le vecteur de coordonnées f'(t) et g'(t) est un vecteur directeur de la tangente au point de coordonnées f(t) et g(t).

[jass73110]

Bonjour nuage et merci d'avoir répondu a mon ennoncé.
j'ai pas trop saisi se que tu m'as mis.
Je vais te mettre se que j'ai compris!
je calcule les dérivée:
donc
f'(t)=-2t+4
g'(t)=-4t+2
ensuite avec ses deux equations il fautque je vérifi qu'en A(1,1) c'est bien un point de tangente à la courbe T!
Je serais tenter de mettre f'(t)=1 dans les deux cas de meme avec g'(t), pour trouver le coeficient directeur, je l'ai fait et je trouve pour f un coeficient directeur de -5/2 et pour g de 1/4!
mais bon je pense que je part mal car je vais finir par calculer une droite corespondant à une tangente pour chaque courbe f et g au point x=1.
Tu pourais me détailler un peu plus si tu as un peu de temps devant toi.
J'aimerais bien connaitre la solution! et le truc qui m'intrigue c'est qu'ilsnous demande de montrer que le point A est tangente et non de calculer cette tangente!!
Merci pour ton aide
JASS

[nuage]

Le point A est donné par t=0.
La tangente à la courbe a pour vecteur directeur (f'(0);g'(0))=(4;2).
Ce vecteur est bien colinéaire au vecteur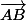 de coordonnées (2;1).
Ce qu'il faut bien comprendre c'est qu'a chaque valeur de t correspond un point de la courbe de coordonnées (f(t);g(t)) et, (sauf points critiques) une tangente de vecteur directeur (f'(t);g'(t)). Mais les coordonnées du point n'interviennent pas dans celles du vecteur directeur.

Je ne suis pas sûr d'avoir été assez clair, mais j'espère que ça 'aidera quand même.

[jass73110]

Merci pour ta réponse!
Je vois le déroulement des opération, mais j'ai un problème pour le point de départ quand tu fixe en A t=0, ou le prend tu le zero! et par exemple en C pour la suite de la question, tu prends quoi pour t?
merci

JASS

[nico74]

On représenter la courbe T de cette manière :

pour tout

et

[nico74]

alors là je ne sais pas comment faire! je sais calculer une tangente sur une courbe classique genr parabole, mais là, une courbe faite de deux courbes!!!
Merci de me donner l'explication. Est ce que c'est du genre Y-X!



Non, il ne faut pas que tu vois ça comme deux courbes.
Imagine la variable t comme étant le temps et la courbe T comme étant la trajectoire d'un point M dans le plan qui à chaque instant t a pour coordonnées


C'est à dire qu en "position initiale" (à l'instant t=0), M(1,1)
A l'instant t=0.23 (par exemple) M(f(0,23),g(0,23)), i.e. M(1,8671;1,3542)
A l'instant t=0.5 (par exemple) M(f(0,5),g(0,5)), i.e. M(3,25;1,5)
A l'instant t=1 (tu peux te dire t= 1 minute) M(4,1) -----> t=1 fin de l'étude de la trajectoire de M


J'espere que j ai été clair. Bon courage

[jass73110]

Merci à vous deux pour vos conseil!
j'ai été un peu long à vous répondre mais grace à vos explication j'ai pu y arriver.
Encore merci
JASS