Besoins d'aide pour une équation

par **maxx58** » 04 Avr 2007, 16:26

Voici mon souci

z=alpha ax²+beta
Determine les coordonnees de B et C pui en deduire les valeure alpha et beta

merci pour votre aide

par **mathelot** » 04 Avr 2007, 20:08

bonsoir,

au vu des courbes, on cherche des équations de la forme:

et

soit en élevant au carré:

ensuite ces courbes passent par les points
E(3,15) et B(5,20) , ce qui donne le système:

par **maxx58** » 04 Avr 2007, 20:12

Et pour trouve alpha et beta on fait comment?

par **fahr451** » 04 Avr 2007, 20:33

maxx58 a écrit:Voici mon souci

z=alpha ax²+beta
Determine les coordonnees de B et C pui en deduire les valeure alpha et beta

merci pour votre aide

bonsoir

c'est codé ou quoi ce problème?

je comprends pas l'énoncé

qui sont B,C z?

j'ai raté la saison 1 ?

par **maxx58** » 04 Avr 2007, 20:38

B et C son de point du dessin B es en ho a droite et z est une equation z=alpha.x²+beta

par **mathelot** » 04 Avr 2007, 20:41

:doh: a écrit:

On fait la différence termes à termes des égalités:

puis on reporte la valeur de

dans une des deux égalités,
pour calculer

par **maxx58** » 04 Avr 2007, 20:45

mai lequation du poin B c pa 20=alpha25+beta???
ou 5=alpha400+beta

On remplace bien x par 5??

par **mathelot** » 04 Avr 2007, 20:52

La concavité des parois est tournée vers l'axe

.
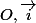
ça ne peut pas être une équation de celles que tu proposes.

par **maxx58** » 04 Avr 2007, 20:56

je comprens plu rien il me dise a partir des coordone de B et C determine alpha et beta

Donc B (5;20) donc lequation est 20=alpha25+beta

Si c pa sa fo aider

par **mathelot** » 04 Avr 2007, 21:05

maxx58 a écrit:Donc B (5;20)

Les coordonnées de B sont exactes.

On cherche l'équation du toit ou des parois (du chateau d'eau) ?
Le problème est que l'ordonnée de C n'est pas connue.

par **maxx58** » 04 Avr 2007, 21:16

oui c bien sa mai o dessu de la cote 20 on a un 1 je croix donc ki servirai de cote pour C mai c mal reprente je trouve donc je dirai que C(0;21)

par **mathelot** » 05 Avr 2007, 07:43

mathelot a écrit:On cherche l'équation du toit ou des côtés ?

peux tu répondre à cette question ?

par **maxx58** » 05 Avr 2007, 12:04

Voici l'enonce:

L'arc BC est un arc de la parabole d'equation z=alpha.x²+beta

determinee les coordonnee de B et C et en deduire les valeurs de alpha et beta

J'ai pas plus dans l'enonce

par **nuage** » 05 Avr 2007, 14:43

Salut,
on a

et on sait que

(point C)et

(point B). Du moins si j'ai bien compris ce qui précède.

Si c'est le cas :

par **maxx58** » 05 Avr 2007, 16:48

oui moi aussi je trouve sa et apres il me demande de transformer z=alpha.x²+beta en x=5racine(21-z) et la je bloque car je trouve x=0.04racine(21-z) et jarrive pa a trouve mon erreur

Besoins d'aide pour une équation

Besoins d'aide pour une équation

Qui est en ligne