Bonjour je ne trouve pas comment calculer les limites suivantes
Limite en ;);) de (x³ - 2x + 3)/(x ln x)
Limite en ;);) de (1-2/x)exposant x
Limite en 0+ de 4x²+(ln x)² - (1/x)
merci de votre aide
Besoin de renseignement
7 messages
- Page 1 sur 1
On a souvent besoin d'utiliser l'assertion suivante: ( x
x 
 : x > 1
: x > 1  x > Ln(x)).
x > Ln(x)).
Soient x et t deux réels tels que x > t > 1, donc on a :
t > 1 1 >
1 > 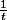 > 0
> 0 
 1 dt >
1 dt > 
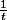 dt >
dt >  x - 1 > Ln(x)
x - 1 > Ln(x)  x - Ln(x) > 1
x - Ln(x) > 1  x - Ln(x) > 0
x - Ln(x) > 0  x > Ln(x),
x > Ln(x),
donc x
x 
 : x > 1
: x > 1  x > Ln(x).
x > Ln(x).
On peut utiliser cette propriété pour calculer
}) .
.
Une petite remarque: x > 1 x > Ln(x)
x > Ln(x) 
}) > 1
> 1 
}) > 1
> 1 
}) > x
> x
et aussi x = +
x = + 


}) = +
= +  .
.
Soient x et t deux réels tels que x > t > 1, donc on a :
t > 1
donc
On peut utiliser cette propriété pour calculer
Une petite remarque: x > 1
et aussi
Pour le calcul de 
)}^2 - \frac{1}{x}) , je crois qu'il est judicieux d'utiliser la formule suivante :
, je crois qu'il est judicieux d'utiliser la formule suivante : )}^2 = 0) .
.
Cette formule s'obtient comme suit:
)}^2) =
= )}^2) =
= )}^2) = 0 puisque
= 0 puisque  = 0) .
.
Vous trouverez ici un cours très intéressant à ce sujet.
Cette formule s'obtient comme suit:
Vous trouverez ici un cours très intéressant à ce sujet.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
