Besoin d'indication (Hilbert et Fourier)

[Patrick.p]

deux question la premeir :

1)

Soit H un Hilbert,
Soient A et B deux s.e.v fermé de H tel que A inter B = {0}
Soit u : AxB -> H
u(x,y) = x+y avec u lineaire continue injective mais u^(-1) non continue.
u^(-1) : Im(u) -> AxB.
Soit E = Im(u).
Quel argument peu me permettre d'affirmé que E n'est pas complet?

2)

Soit f dans L²(T), T = R/Z.
n>=1 et t dans T.
Soit fn(t) := 1/n (Somme de k=0 a n-1 de [ f(t + k/n) ])

Quel argument peu me permettre d'affirmé que :
liminte en n -> inf de fn(t) = l'integrale de f(t) dt sur [0,1]?


En espérant que mes notations soient compréhensible, et qu'aucun n'argument ne manque. Je ne trouve pas de théoréme me donnant ces 2 affirmation.
Merci d'avance, a tous ceux qui auront pris la peine de me lire même sans me répondre.

[tize]

Bonjour,
pour la première question ,je ne sais pas de quel niveau il s'agit mais je pense que l'on peut conclure assez facilement avec le théorème de l'application ouverte (Banach-Schauder ) : "Une application linéaire continue surjective entre deux Banach est ouverte".
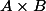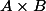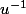Ici, est un banach comme produit de deux banachs (puisque A et B sont fermés dans H banach) u est linéaire continue et surjective sur Im(u)=E (s.e.v. de H logique...) alors si E était complet (fermé dans H) alors u vérifierait les hypothèses du théorème et u serait donc une application ouverte de dans autrement dit serait continue ce qui est en contradiction avec les hypothèses...
Qu'en pensez-vous ?