Bonjour,
Je dois faire cette exercice pour demain et après un certain temps passé dessus il s avère que je n'avance que peu.
Soit A dans M_3(R) telle que A^3 + A = 0,
je dois montrer que A est nulle ou semblable à ((0,0,0), (0,0,-1), (0,1,0)).
J'ai bien essayé d'étudier tout ce qui est polynôme annulateur, et spectre mais je ne vois pas comment lier ça avec le fait de trouver une matrice semblable, j'aurais donc besoin d'un coup de pouce.
Merci d'avance.
Besoin d'aide...
5 messages
- Page 1 sur 1
Re: Besoin d'aide...
Bonsoir !
Puisque tu as un polynôme annulateur, le polynôme minimal est un diviseur de
est un diviseur de ) .
.
Si=X) il vient
il vient 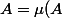=0) .
.
Si=X^2+1) tu as une contradiction en prenant les déterminants.
tu as une contradiction en prenant les déterminants.
Si=X(X^2+1)) tu as une matrice qui est diagonalisable sur le corps des complexes à l'aide d'une matrice de passage complexe
tu as une matrice qui est diagonalisable sur le corps des complexes à l'aide d'une matrice de passage complexe  . En prenant
. En prenant  tu devrais trouver une combinaison
tu devrais trouver une combinaison  inversible telle que
inversible telle que ^{-1}A(M+tN)) soit de la forme que tu souhaites obtenir.
soit de la forme que tu souhaites obtenir.
Puisque tu as un polynôme annulateur, le polynôme minimal
Si
Si
Si
Re: Besoin d'aide...
Au lieu de chercher  tu peux raisonner sur les bases.
tu peux raisonner sur les bases.
tu as une base de vecteurs avec des composantes conjuguées avec
de vecteurs avec des composantes conjuguées avec  et tu cherches des combinaisons de
et tu cherches des combinaisons de  pour avoir
pour avoir 
tu as une base
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
