Besoin d'aide sur les calculs algébriques

[ketchuptomatosauce]

Bonjour,

Je suis en train de faire un exercice et je ne comprends absolument pas la réponse du corrigé, voici l'énoncé:

Pn(x)=∏k=1n(1+xk).
il suffit de résoudre pour x=-n
et je trouve Pn(-n)= 1+( (-n)^n)/n! tandis quele corrigé propose Pn(-n)= 0
Je suis dans la plus grande incompréhension.

Merci d'avance!!

[Ben314]

Salut,
Si alors il est bien clair que les racines de sont et comme 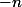n'en fait pas partie (sauf si 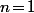) c'est que

Si tu donnais l'énoncé de ton exo., ça aiderais grandement à comprendre d'où vient le problème.
Sinon, as-tu cherché à le résoudre cet exercice ? (En math, lire des corrections d'exercice, ça sert à rien si on a pas soit-même longuement cherché la solution).

[ketchuptomatosauce]

Bonsoir,

Merci beaucoup de votre aide, en essayant simplement d'écrire le produit sous forme de pointillés j'ai compris qu'il était égal à zéro ( l'énoncé s'est déformé lors du copié-collé):
Pn(x)= 1+ x/k , k appartenant à (1, n) et pour x=-n
d'où Pn(-n)= (1-n)(1-n/2)...(1-n/n)
= (1-n)(1-n/2)...(1-1)
= 0
Tout simplement !

Merci quand même